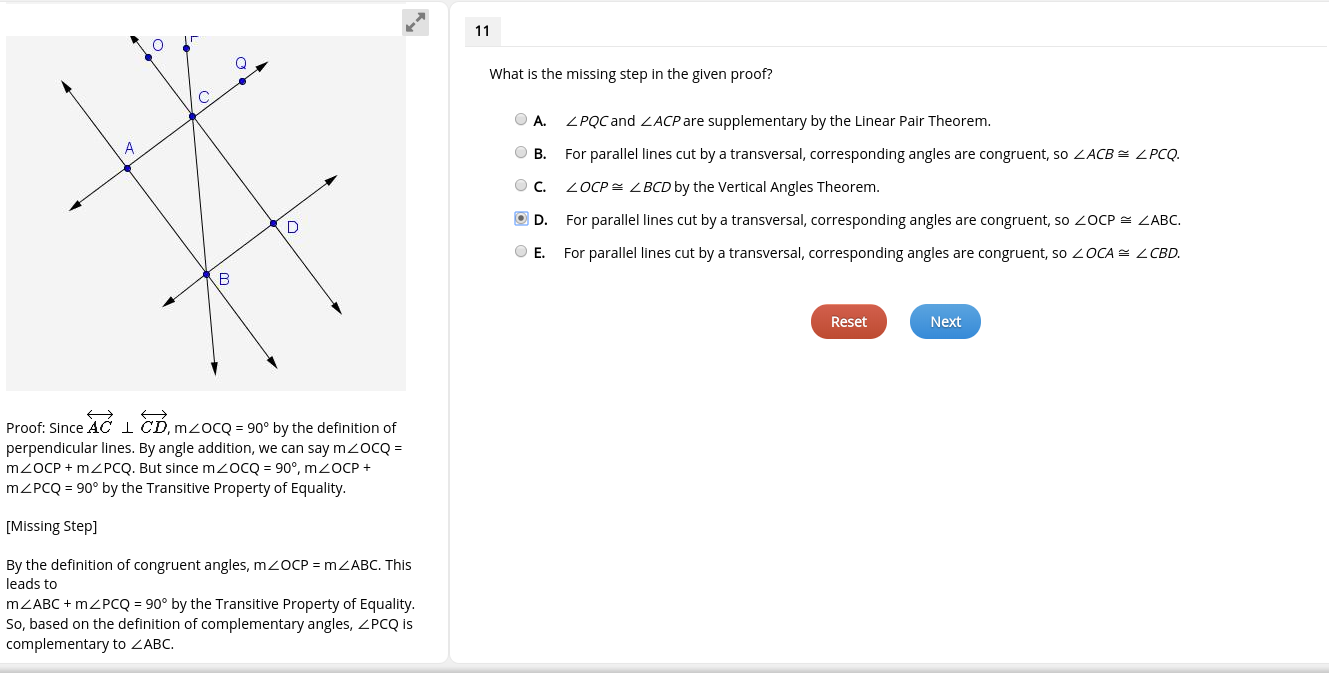
A B D Proof: Since AC LCD, moc: mZOCQ Proof: Since AC 1 CD, mzocQ = 90 by the definition of perpendicular lines. By angle addition, we can say mzocQ= mZOCP+mZPCQ. But since mZOCQ = 90, mZOCP + mZPCQ = 90 by the Transitive Property of Equality. [Missing Step] By the definition of congruent angles, mZOCP = m/ABC. This leads to m/ABC+mZPCQ = 90 by the Transitive Property of Equality. So, based on the definition of complementary angles, ZPCQ is complementary to ZABC. 11 What is the missing step in the given proof? A. B. . C. OD. O E. ZPQC and ZACP are supplementary by the Linear Pair Theorem. For parallel lines cut by a transversal, corresponding angles are congruent, so ZACB = ZPCQ. ZOCP= ZBCD by the Vertical Angles Theorem. For parallel lines cut by a transversal, corresponding angles are congruent, so ZOCP = ZABC. For parallel lines cut by a transversal, corresponding angles are congruent, so ZOCA = Z CBD. Reset Next