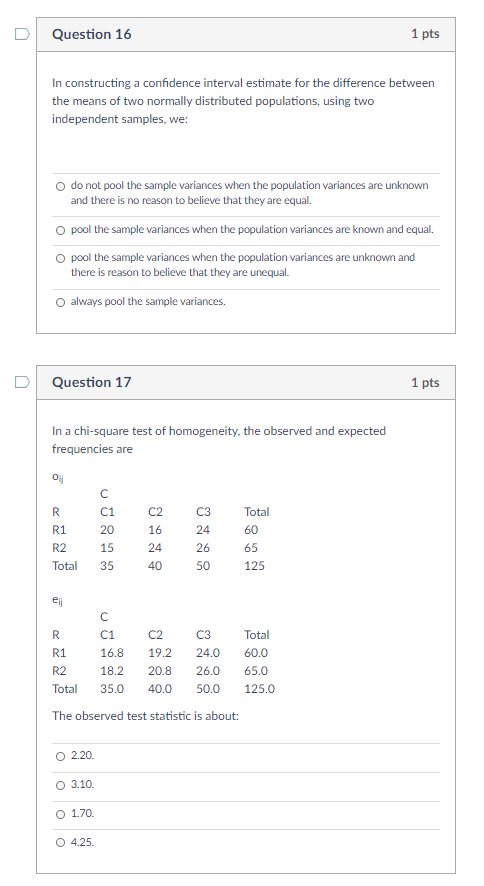
D Question 16 1 pts In constructing a confidence interval estimate for the difference between the means of two normally distributed populations, using two independent samples, we: O do not pool the sample variances when the population variances are unknown and there is no reason to believe that they are equal. O pool the sample variances when the population variances are known and equal. O pool the sample variances when the population variances are unknown and there is reason to believe that they are unequal. O always pool the sample variances. D Question 17 1 pts In a chi-square test of homogeneity, the observed and expected frequencies are C R C1 C2 C3 Total R1 20 16 24 60 R2 15 24 26 65 Total 35 40 50 125 el C R C1 C2 C3 Total R1 16.8 19.2 24.0 60.0 R2 18.2 20.8 26.0 65.0 Total 35.0 40.0 50.0 125.0 The observed test statistic is about: O 2.20. O 3.10. O 1.70. O 4.25.D Question 18 1 pts Suppose that we reject a null hypothesis at the 2.5% level of significance. For which of the following c-values do we also reject the null hypothesis? O 0.05. O 0.01. O 0.005. O 0.0025. D Question 19 1 pts In one-way ANOVA, suppose that there are five treatments with n1 = ny = ng = 5 and n14 = n; = 7. Then the mean square for error, MSE, equals: O SSE/4. O SSE/29. O SSE/5. O SSE/24. D Question 20 1 pts A survey will be conducted to compare the grade point averages of US high-school students from four different school districts. Students are to be randomly selected from each of the four districts and their grade point averages recorded. The ANOVA model most likely to fit this situation is: O one-way ANOVA based on independent samples. O two-way ANOVA based on independent samples. O one-way ANOVA based on randomised blocks. O random effects ANOVA