data structures and algorithm

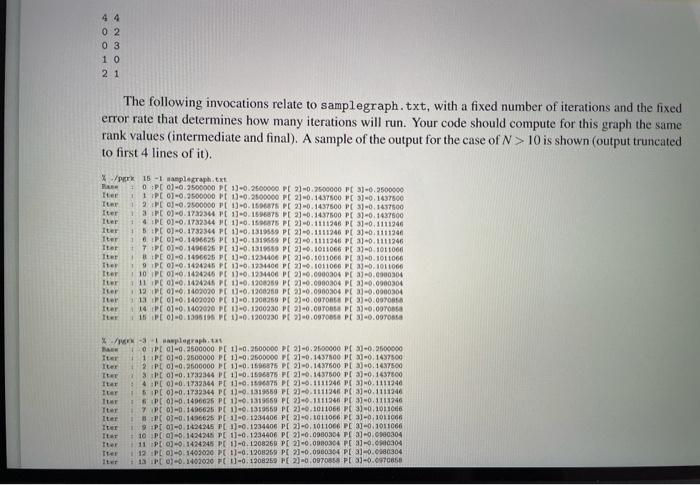
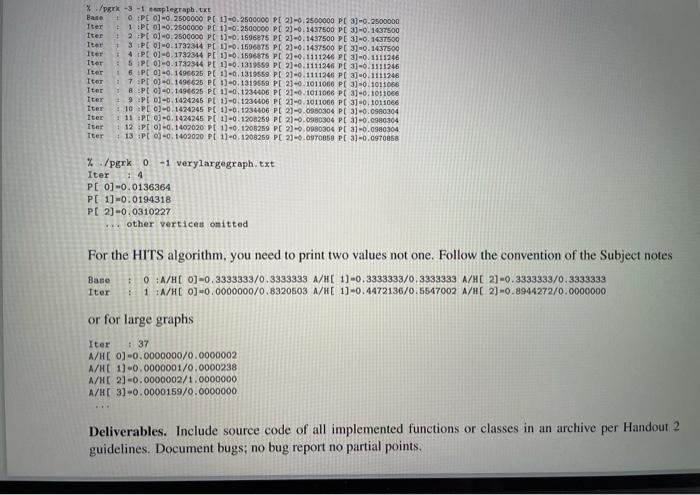
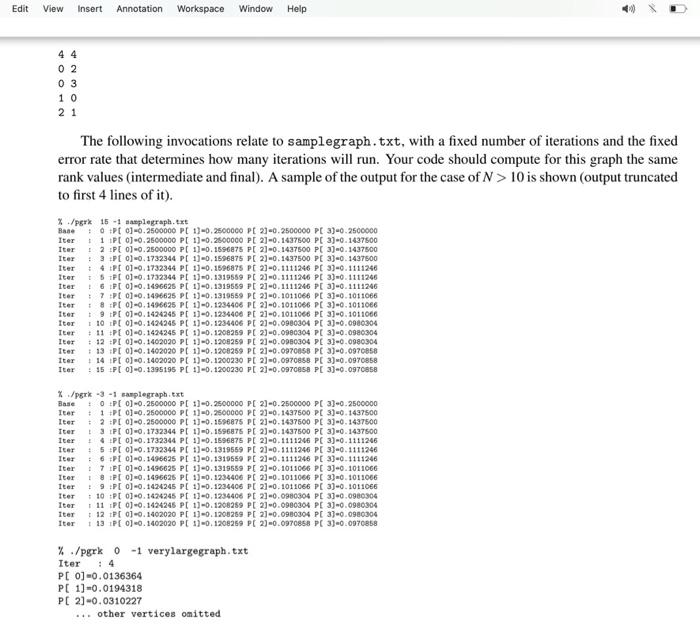
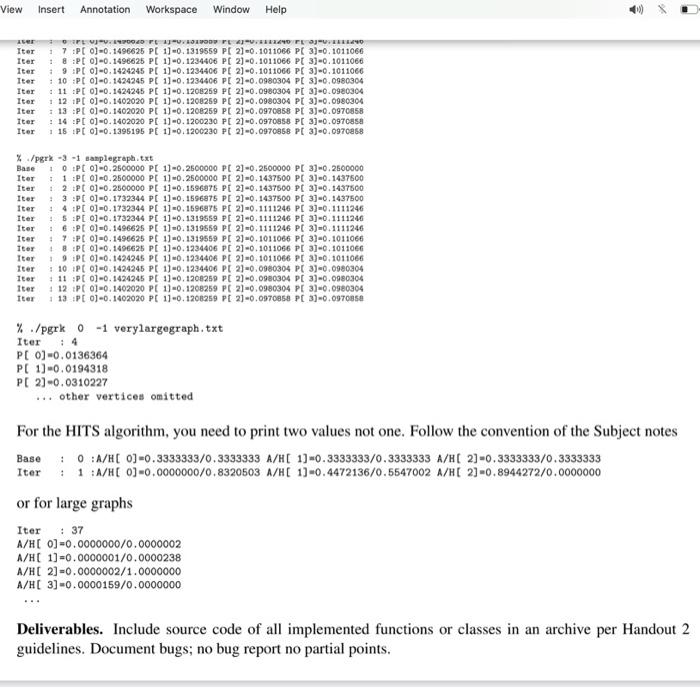
Implement Kleinberg's HITS Algorithm, and Google's PageRank algorithm in Java, Cor C++ as explained. (A) Implement the HITS algorithm as explained in class/Subject notes adhering to the guidelines of Handout 2. Pay attention to the sequence of update operations and the scaling. For an example of the Subject notes, you have output for various initialization vectors. You need to implement class or function hits (e.g. hitsWXYZ. For an explanation of the arguments see the discussion on PageRank to follow. % java hita iterations initialvalue filename % Vita iterations initialvalue file (B) Implement Google's PageRank algorithm as explained in class/Subject notes adhering also to the guidelines of Handout 2 and this description. The input for this and the previous) problem would be a file containing a graph represented through an adjacency list representation. The command-line interface is as follows. First we have the class/binary file (eg pgrk). Next we have an argument that denotes the number of iterations if it is a positive integer or an errorrate for a negative or zero integer value. The next argument initialvalue indicates the common initial values of the vector(s) used. The final argument is a string indicating the filename that stores the input graph, % /park 1toration initialvalue filemane // in fact PrWXYZ % java per iteration initialvalue filenane // in fact Per VXYZ The two algorithms are iterative. In particular, at iteration / all pagerank values are computed using results from iteration : - 1. The initialvalue helps us to set up the initial values of iteration 0 as needed. Moreover, in PageRank, parameter d would be set to 0.85. The PageRank PR(A) of vertex A depends on the PageRanks of vertices Ti....Tincident to A. i.e. pointing to A; check Subject 7 section 3.6 for more details. The pageranks at iteration I use the pageranks of iteration 1 -1 (synchronous update). Thus PRCA) on the left in the PageRank equation is for iteration 1, but all PR (T) values are from the previous iteration 1-1. Be careful and synchronize! In order to run the 'algorithm' we either run it for a fixed number of iterations and iterations determines that, or for a fixed errorrate (an alias for iterations); an iterations equal to 0 corresponds to a default errorrate of 10-A-1, -2, etc -6 for iterations becomes an errorrate of 10-10-2..., 10- respectively. At iteration when all authority/hub/PageRank values have been computed (and auth/hub values scaled) we compare for every vertex the current and the previous iteration values. If the difference is less than errorrate for EVERY VERTEX, then and only then can we stop at iteration 1. . Subject / section 3.6 for more details. The pageranks at iteration I use the pageranks of iteration 1 -1 (synchronous update). Thus PR(A) on the left in the PageRank equation is for iteration 1, but all PR (T) values are from the previous iteration 1-1. Be careful and synchronize! In order to run the 'algorithm' we either run it for a fixed number of iterations and iterations determines that, or for a fixed errorrate (an alias for iterations): an iterations equal to 0 corresponds to a default errorrate of 10-5. A-1, -2, etc. -6 for iterations becomes an errorrate of 10-1,10-2,..., 10-6 respectively. At iteration t when all authority/hub/PageRank values have been computed (and auth/hub values scaled) we compare for every vertex the current and the previous iteration values. If the difference is less than errorrate for EVERY VERTEX, then and only then can we stop at iteration 1, Argument initialvalue sets the initial vector values. If it is Othey are initialized to 0, if it is 1 they are initialized to 1. If it is -1 they are initialized to 1/N, where N is the number of web pages (vertices of the graph). If it is -2 they are initialized to 1/ N. filename first.) Argument filename describes the input (directed) graph and it has the following form. The first line contains two numbers: the number of vertices followed by the number of edges which is also the number of remaining lines. PAY ATTENTION THAT NUMBER OF VERTICES comes first. The sample graph is treacherous: n and m are the same! All vertices are labeled 0,...,N-1. Expect N to be less than 1,000,000. In each line an edge (ij) is represented by i j. Thus our graph has (directed) edges (0,2),(0,3), (1.0).(2,1). Vector values are printed to 7 decimal digits. If the graph has N GREATER than 10, then the values for iterations, initialvalue are automatically set to 0 and -1 respectively. In such a case the hub/authority/pageranks at the stopping iteration (.et) are ONLY shown, one per line. The graph below will be referred to as samplegraph.txt 02 0 3 10 21 The following invocations relate to samplegraph.txt, with a fixed number of iterations and the fixed error rate that determines how many iterations will run. Your code should compute for this graph the same rank values (intermediate and final). A sample of the output for the case of N > 10 is shown (output truncated to first 4 lines of it). % / 15 - 1 samplegraph.txt + OPC 0-0.2500000 PE 1-0.2600000 PC 2-0.2500000 PC 3-0.2500000 Iter 11 P 0-0.9500000 P 1-0.2500000 PC 20.14.97500 PC 3-0.1437500 Iter 19 PE 0-0.9500000 PE 1)-0.167 PC 2-0.1437500 PC 3-0.1437500 Iter 1. 3 I 06.1732344 PE10.17 PL 21 -0.1437500 PC 3-0.1437500 Iuer 14 PE 0-0.1782344 FC 1-0. 1596875 PC 20.1111246 PC 3-0.1111246 Iter SPEC. 1732544 PC 1)-0.1319559 PE 21 -0.1111246 PC 3-0.1111240 tter 8PCO-0.1496625 PC 1-0.1318159 PC 20.1111246 PE30.1111246 + 7 PC 0-0 1406626 PE 19-0.131959 PE 21-01011066 PC 3-0.1011001 TERT PE0)-0.1496025 PC 1-0:123406 PC 21-01011006 PC -0.1011066 ter PC 0-0 1424246 PE 11-0.1934400 PC21.1011000 PE-0.1011006 Iter 10 PE 01-0. 1424246 PE 170.124406 P[ 2-0.0000304 31-0.900304 Iter 11 PE 0-0 1424246 PL 1)-0.1909089 P 21-0.0980304 PL 3-0.0000304 Iter 12 0.1109020 P 1-0.1200260 PE 3.0900304 PC 1-0.0000304 Iter 113 Pt 0) 0.1409020 PE 1.0.1908259 PC 20.00TC PC 30.097 Iter 11 P 001402020 PO 1-0.1300230 PL 20.00TOP 2) 0.00708 18 PE 01-01305195 E 1)-0.1200030 PC 10.0970068 PC 3-0.0970 */ -3 plegraph. 10 P 0-0.3500000 PE 1)-0.2500000 P 23-0.2500000 PE 3-0 2500000 Iter 1 PE 0-0 2500000 PE 1) - 2500000 PC 21-0.1437500 PE 3-0.147500 Iter 2.PL 0 -0.2500000 PE 1-0.1506875 PC 2-0.1437500 PE 3-0.1437500 Iter PC 0-0, 1732344 PC 10.1175 PC 2-0.1437500 PE 3)-0.1437800 Itar 4 PE 0-0. 1732344 PC 1-0.15278 PE 2-.1111246 PE 30.1111340 Ttar TSP 0-0 1732344 PC 1-0.1314559 PE 2-0.1111248 PC 30.1111246 1 0 -0.1496625 PL 11-131959 PC 20.11112461 PO 3-0.1111246 Tter i7Pt 0-0.1496625 Pt 1)-0.1319559 PE 23.1011066 Pt 31-01011046 Iter 1 PC 0-0.1496625 PC 101234406 PT 2) - 11066 PE 31-01011006 Iter Pt 01-0.1426245 PL 1). 1934406 PE 23-0, 1011066 PE 31-01011066 + 10 P[0] -0.1424245 PE 1-0.1234406 PE 21-0.0000304 PE 31-0.0100304 Iter 11 PL 0-0.1424245 PE 11-01208269 PC 20.09.04 PC 3-0.0304 12 PC -0.1403000 PC 11-0.1200269 PL 23-0.0980304 PE 31-0.0160304 Iter # 18 PC 0-0.1402030 FC 1-0. 1908259 PE 20.0970558 PE 31-0.9705 /park -3 -1 samplegraph.txt Baile OPC 0 0.2500000 PC 1] -0.2500000 PC 2] -0.2500000 P 3) 0.2500000 Iter 1 Pt 0] -0.2500000 PE 11-0.2500000 PE 2) -0.1437500 PE 3) -0.1437500 Iter 2 Pt 0-0.250C0OO PE 0.1596875 PC 2-0.1437500 PE 3-0.1437500 Tter 1 3 Pt 0-0. 1732314 PC 13-0.1606875 P[ 2)-0.1437500 PC 3-0.1437500 Iter 4 Pt 0-6.1731314 PC 10.1596875 PC 2-0.1111246 PC 3-0.1111246 Iter : 5 IPL 0)-0.1739344 PC 1)-0.131959 PE 2-0.1111246 PE 3-0.1511246 Iter 6 PC 0-0 1496625 PC 1] -0.1319559 PC 21-0. 1111246 PC 3] -0.1111246 Iter 2 7 Pt 0-0.1496625 PC 1)-0.1319569 PC 23-0.1011066 PC 31-01011056 Iter 1 Pt 0)-0.1496625 PE 11-0.1234406 PC 2-0.1011066 PC 31-0.1011056 Iter 9 Pt 01-0. 1424245 PC 1-0. 1234406 PE 21-0.1011066 PC 3-0.1011006 Iter 1 10 PC 0-0. 1424245 PL 11-01234406 PC 21-0.0980304 PC 3] -0.0980304 iter 1 11 PC 0-0 1424245 Pt 1)-0.1200259 PC 2-0.0980304 PC 3] -0.0980304 iter 12 Pt 0-01402030 PC 1)-0.1208259 PC2-00304 PL 31-0.0980304 tter + 13 P 0-0, 1402090 PE 11-0, 1206259 PC 2-6.970058 PC 31-0.0970858 % /pgrk 0-1 verylargegraph.txt Iter P[ 0] -0.0136364 PC 11-0.0194318 P[ 2-0.0310227 other vertices omitted For the HITS algorithm, you need to print two values not one. Follow the convention of the Subject notes Bano 0 :A/H[0] -0.3333333/0.3333333 A/H[ 1)-0.3333333/0.3333333 A/HE 2] -0.3333333/0.3333333 Iter 1 N/H[0]=0.0000000/0.8320503 A/H[ 11-0.4472136/0.5547002 A/H[ 23-0.8944272/0.0000000 + or for large graphs Iter + 37 A/H[0] -0.0000000/0.0000002 A/HC 1)-0.0000001/0.0000238 A/H[ 2] -0.0000002/1.0000000 A/HC 3] -0.0000159/0.0000000 Deliverables. Include source code of all implemented functions or classes in an archive per Handout 2 guidelines. Document bugs, no bug report no partial points. tice File Edit View Insert Annotation Workspace Window Help Q 2 IR NIVES SENSE SENWES CA iterations initialvalue filename (A) Implement the HITS algorithm as explained in class/Subject notes adhering to the guidelines of Handout 2. Pay attention to the sequence of update operations and the scaling. For an example of the Subject notes, you have output for various initialization vectors. You need to implement class or function hits (e.g. hitsWXYZ. For an explanation of the arguments see the discussion on PageRank to follow. % java hits iterations initialvalue filename % ./hits (B) Implement Google's PageRank algorithm as explained in class/Subject notes adhering also to the guidelines of Handout 2 and this description. The input for this and the previous) problem would be a file containing a graph represented through an adjacency list representation. The command-line interface is as follows. First we have the class/binary file (eg pork). Next we have an argument that denotes the number of iterations if it is a positive integer or an errorrate for a negative or zero integer value. The next argument initialvalue indicates the common initial values of the vector(s) used. The final argument is a string indicating the filename that stores the input graph. % /perk iteration initialvalue 11lenane // in fact pgrXWXYZ X java perk iterations initialvalue filene // in fact perkWXYZ The two algorithms are iterative. In particular, at iteration tall pagerank values are computed using results from iteration - 1. The initialvalue helps us to set-up the initial values of iteration 0 as needed. Moreover, in PageRank, parameter d would be set to 0.85. The PageRank PR(A) of vertex A depends on the PageRanks of vertices Ti...... incident to A. i.e. pointing to A; check Subject 7 section 3.6 for more details. The pageranks at iteration I use the pageranks of iteration : - 1 (synchronous update). Thus PR(A) on the left in the PageRank equation is for iteration 1, but all PR (T) values are from the previous iteration 1-1. Be careful and synchronize! In order to run the algorithm' we either run it for a fixed number of iterations and iterations determines that, or for a fixed errorrate (an alias for iterations); an iterations equal to 0 corresponds to a default errorrate of 10-5.A-1, -2, etc , -6 for iterations becomes an errorrate of 10-10-2... 10 respectively. At iteration / when all authority/hub/PageRank values have been computed (and auth/hub values scaled) we compare for every vertex the current and the previous iteration values. If the difference is less than errorrate for EVERY VERTEX, then and only then can we stop at iteration 1. Argument initialvalue sets the initial vector values. If it is Othey are initialized to 0, if it is 1 they are initialized to 1. If it is -1 they are initialized to 1/N, where N is the number of web pages (vertices of the graph). If it is -2 they are initialized to 1/VN. filename first.) e Edit View Insert Annotation Workspace Window Help >> comamng a graper represeme unough an aujacency is representation. The command-tme merace is as follows. First we have the class/binary file (eg pgrk). Next we have an argument that denotes the number of iterations if it is a positive integer or an errorrate for a negative or zero integer value. The next argument initialvalue indicates the common initial values of the vector(s) used. The final argument is a string indicating the filename that stores the input graph. %/pgrk iterations initialvalue filename // in fact pgrkwXYZ % java pgrk iterations initialvalue filename // in fact pgr&WXYZ The two algorithms are iterative. In particular, at iteration all pagerank values are computed using results from iteration : - 1. The initialvalue helps us to set-up the initial values of iteration 0 as needed. Moreover, in PageRank, parameter d would be set to 0.85. The PageRank PR(A) of vertex A depends on the PageRanks of vertices Ti....... incident to A, i.e. pointing to A; check Subject 7 section 3.6 for more details. The pageranks at iteration / use the pageranks of iteration - 1 (synchronous update). Thus PR(A) on the left in the PageRank equation is for iteration t, but all PR (T) values are from the previous iteration 1-1. Be careful and synchronize! In order to run the 'algorithm' we either run it for a fixed number of iterations and iterations determines that, or for a fixed errorrate (an alias for iterations); an iterations equal to 0 corresponds to a default errorrate of 10-5 A-1, -2, etc , -6 for iterations becomes an errorrate of 10-10-2,...,10-respectively. At iteration when all authority/hub/PageRank values have been computed (and auth/hub values scaled) we compare for every vertex the current and the previous iteration values. If the difference is less than errorrate for EVERY VERTEX, then and only then can we stop at iteration 1. Argument initialvalue sets the initial vector values. If it is Othey are initialized to 0. if it is 1 they are initialized to 1. If it is -1 they are initialized to 1/N, where N is the number of web-pages (vertices of the graph). If it is -2 they are initialized to 1/VN. filename first.) Argument filename describes the input (directed) graph and it has the following form. The first line contains two numbers: the number of vertices followed by the number of edges which is also the number of remaining lines. PAY ATTENTION THAT NUMBER of VERTICES comes first. The sample graph is treacherous: n and m are the same! All vertices are labeled 0,...,N-1. Expect N to be less than 1,000,000. In each line an edge (ij) is represented by i j. Thus our graph has (directed) edges (0,2),(0,3), (1,0),(2,1). Vector values are printed to 7 decimal digits. If the graph has N GREATER than 10, then the values for iterations, initialvalue are automatically set to O and -1 respectively. In such a case the hub/authority/pageranks at the stopping iteration (i.et) are ONLY shown, one per line. The graph below will be referred to as samplegraph.txt Edit View Insert Annotation Workspace Window Help 44 02 03 10 21 The following invocations relate to samplegraph.txt, with a fixed number of iterations and the fixed error rate that determines how many iterations will run. Your code should compute for this graph the same rank values (intermediate and final). A sample of the output for the case of N > 10 is shown (output truncated to first 4 lines of it). %./perk 15 -1 nasplegraph.txt Base OPC 0] -0.2500000 PE 11-0.2500000 PE 23-0.2500000 PE 3)-0.2500000 Iter # 1 P 0-0.2500000 Pt 1)-0.25000GO P[ 21-0.1437500 Pt 3)-0.1437500 Iter I 2PC 0] -0.2500000 PC 1)-0.1596875 P[ 2] -0.1437500 P 3)-0.1437500 Iter # 3 PI 0)-0.1732344 PL 1)-0.1596875 PC 2) -0.1437500 PE 33-0.1437500 Iter 4 PI 03-0.1732344 PE :)-0.1596875 PT 2)-0.1111246 PE 33-0.1111246 Iter 1 SP 0-0.1732344 PL 1)-0.1319559 Pt 2) -0.1111246 PE 33-0.1111246 Iter 670)-0.1496625 Pt 1)-0.1319559 PC 2-0.1111246 PC 3)-0.1111246 Iter 7 P 0) 0.1496625 PL 1)-0.1319559 PE 2) -0.1011066 PC 3)-0.1011066 Iter 8PCO)-0.1496625 PE 1)-0.1234406 P[ 2] -0.1011066 PE 3)-0.1011066 Iter 19 PI 01-0.1424245 Pt 1)-0.1234406 PC 21-0.1011066 PE 33-0.1011006 Iter 10 PL 03-0.1424245 Pt 1)-0.1234406 PT 2) -0.0980304 PC a)-0.0980304 Iter 11 PE 0] -0.1424245 PC :) -0.1208259 PC 2)-0.0980304 PL 3)-0.0980304 Iter 12 PI 03-01402090 PE 1)-0.1208259 PE 21-0.0980304 PE 3)-0.0980304 Iter : 13 PI 03-0.1402020 PE 11-01208259 PE 21-0.0970858 PC 3)-0.0970858 Iter 14 P[00.1402020 PO 1)-0.1200230 P[ 2) -0,0970858 PC 3)-0.0970858 Iter 15 :P[ 0-0.1395195 PC 1)-0.1200230 PC 23-0.0970858 PC 33-0.0970858 */perk -3 -1 samplegraph.txt Base OP[0] -0.2500000 PC :)-0.2500000 PC 2)-0.2500000 P 3)-0.2500000 Iter # 1 P 0-0.2500000 PC 1)-0.2500000 PE 23-0.1437500 PC 3)-0.1437500 Iter + 2 PE 0-0.2500000 PE 1)-0.1596875 PE 23-0.1437500 PE 33-0.1437500 Iter 3 [0] -0.1732344 Pt 1)-0.1596875 PC 2) -0.1437500 PT 3)-0.1437500 Iter PC)-0.1732344 PL 1)-0.1596875 PL 21-0.1111246 PC 3)-0.1111246 Iter 5 P[ ] 0.1732344 PC )-0.1319559 PC 2)-0.1111246 PC 3)-0.1111246 Iter 6 Pt 03-0.1496625 PE 1)-0.1319559 PE 2)-0.1111246 PE 33-0.1111246 Iter 17 PC 0-0.1496625 Pt 1)-0.1319559 P[ 2] -0.1011006 PC 3)-0.1011066 Iter 18 PE 0.1496625 PC 1)-0.1234406 PC 2)=0.1011066 PC 30.1011066 Iter : 9 :P[0] -0.1424245 PL 1)-0.1234406 PC 2] -0.1011066 PC 3)-0.1011066 Iter 10 PL 03-0.1424245 PE 1)-0.1234406 PC 2-0.0980304 PL 31-0.0980304 Iter 111 Pt 0-0.1424245 PC 1-0.1208259 PT 2) -0.0200304 PE 3-0.0980304 Iter 12 PI 0-0.1402020 P[ 1)-0.1208269 P[ 2] -0.0980304 PE 33-0.0980304 Iter 113 PE 0-0.1402020 PC 11-01208259 PT 2)-0.0970858 PC 3)-0.0070858 % /pgrk 0 -1 verylargegraph.txt Iter P[0] -0.0136364 P[ 1)-0.0194318 P[ 2] -0.0310227 ... other vertices omitted View Insert Annotation Workspace Window Help Iter Iter Iter Iter Iter Iter Iter Iter Iter OLVENDE VOOR EEN FOUVERN 17 PC 0)-0.1496625 PC 1] -0.1319559 Pt 2) -0.1011066 PC 3)-0.1011066 18:P[0] -0.1496625 PC 1] -0.1234406 PC 2) -0.1011066 PC 3)-0.1011066 + 9 P[0] -0.1424245 P[ 1] -0.1234406 PE 2) -0.1011066 PC 3)-0.1011066 10 :P[ 01-0.1424245 PL 11-0. 1234406 PC 21-0.0980304 PL 3)-0.0980304 : 11 :P[0] -0.1424245 PC 1] -0.1206259 Pt 2) -0.0980304 PL 3)-0.0980304 1 12 P[0] -0.1402020 PC 1] -0.1208259 PC 2) -0.0980304 PC 3)-0.0980304 + 13 :P[0)-0.1402020 PC 11-0.1206259 PC 2) -0.0970858 PC 3)-0.0970858 : 14 Pt 0)-0.1402020 PL 1)-0.1200230 PC 21 -0.0970858 PC 3)-0.097c8s 1 15 PC 0)-0.1395195 PC 1] -0.1200230 Pt 2)-0.0970858 PC 3)-0.0970858 Iter Iter % /perk -3 -1 samplegraph.txt Base 1 OP 0)-0.2500000 PE 1) -0.2600000 PC 2-0.2500000 PC 3)-0.2500000 Iter 1 PC 0 -0.2500000 PC 11-0.2500000 PC 2) -0.1437500 PC 3) -0.1437500 2 PC 0 -0.2500000 PC 1-0.1596876 Pt 2)-0.1437600 PT 3)-0.1437500 Iter 3 :P0) 0.1732344 PC 1)-0.1596875 PE 2] -0.1437500 PC 33-0.1437500 + 4 PC 03-0.1732344 PC 1)-0.1696875 Pt 2)=0.1111246 PC 3)-0.1111246 Iter SPE0)-0.1732344 PC 11-0.1319559 PC 2] -0.1111246 PC 3)-0.1111246 Iter : 6P 0) 0.1496625 Pt 1)-0.1319559 PC 2-0.1111246 Pt 3)-0.1111246 Iter : :P[0] -0.1496625 Pt 1)-0.1319559 PC 2)-0.1011066 PC 3)-0.1011066 Iter 8PC0] -0.1496625 Pt 1)-0.1234406 PT 2) -0.1011066 PC 3)-0.1011066 Iter 1 9 PC 0-0. 1424245 PL 11-0. 1234406 PC 21-01011066 PC 3-0.1011066 Iter 110 PC 0-0.1424245 Pt 1)-0.1234406 PT 2)=0.0980304 PC 3)-0.0980304 Iter 11 PC 0-0.1424245 PL 11 -0.1208259 PC 2) -0.0980304 Pt 3)-0.0980304 Iter # 12 PC 0-0.1402020 PC 1)-0.1208259 PC 21-0.0980304 PE 3)-0.0980304 Iter 13:P[ 0-0.1402020 PC 11-0.1206259 PT 2) -0.0970858 PC 3)-0.097085 % /pgrk 0-1 verylargegraph.txt Iter PE0)-0.0136364 PC 1)-0.0194318 P[ 23-0.0310227 ... other vertices omitted For the HITS algorithm, you need to print two values not one. Follow the convention of the Subject notes Base0 :A/H( 0)-0.3333333/0.3333333 A/H[ 11-0.3333333/0.3333333 A/H[ 23-0.3333333/0.3333333 Iter : 1 :N/H[0)-0.0000000/0.8320503 M/H[ 13-0.4472136/0.5547002 A/H[ 23-0.8944272/0.0000000 or for large graphs Iter : 37 A/H[0]=0.0000000/0.0000002 A/HC 1]=0.0000001/0.0000238 A/H[2] =0.0000002/1.0000000 A/H[ 3)-0.0000159/0.0000000 Deliverables. Include source code of all implemented functions or classes in an archive per Handout 2 guidelines. Document bugs; no bug report no partial points. Implement Kleinberg's HITS Algorithm, and Google's PageRank algorithm in Java, Cor C++ as explained. (A) Implement the HITS algorithm as explained in class/Subject notes adhering to the guidelines of Handout 2. Pay attention to the sequence of update operations and the scaling. For an example of the Subject notes, you have output for various initialization vectors. You need to implement class or function hits (e.g. hitsWXYZ. For an explanation of the arguments see the discussion on PageRank to follow. % java hita iterations initialvalue filename % Vita iterations initialvalue file (B) Implement Google's PageRank algorithm as explained in class/Subject notes adhering also to the guidelines of Handout 2 and this description. The input for this and the previous) problem would be a file containing a graph represented through an adjacency list representation. The command-line interface is as follows. First we have the class/binary file (eg pgrk). Next we have an argument that denotes the number of iterations if it is a positive integer or an errorrate for a negative or zero integer value. The next argument initialvalue indicates the common initial values of the vector(s) used. The final argument is a string indicating the filename that stores the input graph, % /park 1toration initialvalue filemane // in fact PrWXYZ % java per iteration initialvalue filenane // in fact Per VXYZ The two algorithms are iterative. In particular, at iteration / all pagerank values are computed using results from iteration : - 1. The initialvalue helps us to set up the initial values of iteration 0 as needed. Moreover, in PageRank, parameter d would be set to 0.85. The PageRank PR(A) of vertex A depends on the PageRanks of vertices Ti....Tincident to A. i.e. pointing to A; check Subject 7 section 3.6 for more details. The pageranks at iteration I use the pageranks of iteration 1 -1 (synchronous update). Thus PRCA) on the left in the PageRank equation is for iteration 1, but all PR (T) values are from the previous iteration 1-1. Be careful and synchronize! In order to run the 'algorithm' we either run it for a fixed number of iterations and iterations determines that, or for a fixed errorrate (an alias for iterations); an iterations equal to 0 corresponds to a default errorrate of 10-A-1, -2, etc -6 for iterations becomes an errorrate of 10-10-2..., 10- respectively. At iteration when all authority/hub/PageRank values have been computed (and auth/hub values scaled) we compare for every vertex the current and the previous iteration values. If the difference is less than errorrate for EVERY VERTEX, then and only then can we stop at iteration 1. . Subject / section 3.6 for more details. The pageranks at iteration I use the pageranks of iteration 1 -1 (synchronous update). Thus PR(A) on the left in the PageRank equation is for iteration 1, but all PR (T) values are from the previous iteration 1-1. Be careful and synchronize! In order to run the 'algorithm' we either run it for a fixed number of iterations and iterations determines that, or for a fixed errorrate (an alias for iterations): an iterations equal to 0 corresponds to a default errorrate of 10-5. A-1, -2, etc. -6 for iterations becomes an errorrate of 10-1,10-2,..., 10-6 respectively. At iteration t when all authority/hub/PageRank values have been computed (and auth/hub values scaled) we compare for every vertex the current and the previous iteration values. If the difference is less than errorrate for EVERY VERTEX, then and only then can we stop at iteration 1, Argument initialvalue sets the initial vector values. If it is Othey are initialized to 0, if it is 1 they are initialized to 1. If it is -1 they are initialized to 1/N, where N is the number of web pages (vertices of the graph). If it is -2 they are initialized to 1/ N. filename first.) Argument filename describes the input (directed) graph and it has the following form. The first line contains two numbers: the number of vertices followed by the number of edges which is also the number of remaining lines. PAY ATTENTION THAT NUMBER OF VERTICES comes first. The sample graph is treacherous: n and m are the same! All vertices are labeled 0,...,N-1. Expect N to be less than 1,000,000. In each line an edge (ij) is represented by i j. Thus our graph has (directed) edges (0,2),(0,3), (1.0).(2,1). Vector values are printed to 7 decimal digits. If the graph has N GREATER than 10, then the values for iterations, initialvalue are automatically set to 0 and -1 respectively. In such a case the hub/authority/pageranks at the stopping iteration (.et) are ONLY shown, one per line. The graph below will be referred to as samplegraph.txt 02 0 3 10 21 The following invocations relate to samplegraph.txt, with a fixed number of iterations and the fixed error rate that determines how many iterations will run. Your code should compute for this graph the same rank values (intermediate and final). A sample of the output for the case of N > 10 is shown (output truncated to first 4 lines of it). % / 15 - 1 samplegraph.txt + OPC 0-0.2500000 PE 1-0.2600000 PC 2-0.2500000 PC 3-0.2500000 Iter 11 P 0-0.9500000 P 1-0.2500000 PC 20.14.97500 PC 3-0.1437500 Iter 19 PE 0-0.9500000 PE 1)-0.167 PC 2-0.1437500 PC 3-0.1437500 Iter 1. 3 I 06.1732344 PE10.17 PL 21 -0.1437500 PC 3-0.1437500 Iuer 14 PE 0-0.1782344 FC 1-0. 1596875 PC 20.1111246 PC 3-0.1111246 Iter SPEC. 1732544 PC 1)-0.1319559 PE 21 -0.1111246 PC 3-0.1111240 tter 8PCO-0.1496625 PC 1-0.1318159 PC 20.1111246 PE30.1111246 + 7 PC 0-0 1406626 PE 19-0.131959 PE 21-01011066 PC 3-0.1011001 TERT PE0)-0.1496025 PC 1-0:123406 PC 21-01011006 PC -0.1011066 ter PC 0-0 1424246 PE 11-0.1934400 PC21.1011000 PE-0.1011006 Iter 10 PE 01-0. 1424246 PE 170.124406 P[ 2-0.0000304 31-0.900304 Iter 11 PE 0-0 1424246 PL 1)-0.1909089 P 21-0.0980304 PL 3-0.0000304 Iter 12 0.1109020 P 1-0.1200260 PE 3.0900304 PC 1-0.0000304 Iter 113 Pt 0) 0.1409020 PE 1.0.1908259 PC 20.00TC PC 30.097 Iter 11 P 001402020 PO 1-0.1300230 PL 20.00TOP 2) 0.00708 18 PE 01-01305195 E 1)-0.1200030 PC 10.0970068 PC 3-0.0970 */ -3 plegraph. 10 P 0-0.3500000 PE 1)-0.2500000 P 23-0.2500000 PE 3-0 2500000 Iter 1 PE 0-0 2500000 PE 1) - 2500000 PC 21-0.1437500 PE 3-0.147500 Iter 2.PL 0 -0.2500000 PE 1-0.1506875 PC 2-0.1437500 PE 3-0.1437500 Iter PC 0-0, 1732344 PC 10.1175 PC 2-0.1437500 PE 3)-0.1437800 Itar 4 PE 0-0. 1732344 PC 1-0.15278 PE 2-.1111246 PE 30.1111340 Ttar TSP 0-0 1732344 PC 1-0.1314559 PE 2-0.1111248 PC 30.1111246 1 0 -0.1496625 PL 11-131959 PC 20.11112461 PO 3-0.1111246 Tter i7Pt 0-0.1496625 Pt 1)-0.1319559 PE 23.1011066 Pt 31-01011046 Iter 1 PC 0-0.1496625 PC 101234406 PT 2) - 11066 PE 31-01011006 Iter Pt 01-0.1426245 PL 1). 1934406 PE 23-0, 1011066 PE 31-01011066 + 10 P[0] -0.1424245 PE 1-0.1234406 PE 21-0.0000304 PE 31-0.0100304 Iter 11 PL 0-0.1424245 PE 11-01208269 PC 20.09.04 PC 3-0.0304 12 PC -0.1403000 PC 11-0.1200269 PL 23-0.0980304 PE 31-0.0160304 Iter # 18 PC 0-0.1402030 FC 1-0. 1908259 PE 20.0970558 PE 31-0.9705 /park -3 -1 samplegraph.txt Baile OPC 0 0.2500000 PC 1] -0.2500000 PC 2] -0.2500000 P 3) 0.2500000 Iter 1 Pt 0] -0.2500000 PE 11-0.2500000 PE 2) -0.1437500 PE 3) -0.1437500 Iter 2 Pt 0-0.250C0OO PE 0.1596875 PC 2-0.1437500 PE 3-0.1437500 Tter 1 3 Pt 0-0. 1732314 PC 13-0.1606875 P[ 2)-0.1437500 PC 3-0.1437500 Iter 4 Pt 0-6.1731314 PC 10.1596875 PC 2-0.1111246 PC 3-0.1111246 Iter : 5 IPL 0)-0.1739344 PC 1)-0.131959 PE 2-0.1111246 PE 3-0.1511246 Iter 6 PC 0-0 1496625 PC 1] -0.1319559 PC 21-0. 1111246 PC 3] -0.1111246 Iter 2 7 Pt 0-0.1496625 PC 1)-0.1319569 PC 23-0.1011066 PC 31-01011056 Iter 1 Pt 0)-0.1496625 PE 11-0.1234406 PC 2-0.1011066 PC 31-0.1011056 Iter 9 Pt 01-0. 1424245 PC 1-0. 1234406 PE 21-0.1011066 PC 3-0.1011006 Iter 1 10 PC 0-0. 1424245 PL 11-01234406 PC 21-0.0980304 PC 3] -0.0980304 iter 1 11 PC 0-0 1424245 Pt 1)-0.1200259 PC 2-0.0980304 PC 3] -0.0980304 iter 12 Pt 0-01402030 PC 1)-0.1208259 PC2-00304 PL 31-0.0980304 tter + 13 P 0-0, 1402090 PE 11-0, 1206259 PC 2-6.970058 PC 31-0.0970858 % /pgrk 0-1 verylargegraph.txt Iter P[ 0] -0.0136364 PC 11-0.0194318 P[ 2-0.0310227 other vertices omitted For the HITS algorithm, you need to print two values not one. Follow the convention of the Subject notes Bano 0 :A/H[0] -0.3333333/0.3333333 A/H[ 1)-0.3333333/0.3333333 A/HE 2] -0.3333333/0.3333333 Iter 1 N/H[0]=0.0000000/0.8320503 A/H[ 11-0.4472136/0.5547002 A/H[ 23-0.8944272/0.0000000 + or for large graphs Iter + 37 A/H[0] -0.0000000/0.0000002 A/HC 1)-0.0000001/0.0000238 A/H[ 2] -0.0000002/1.0000000 A/HC 3] -0.0000159/0.0000000 Deliverables. Include source code of all implemented functions or classes in an archive per Handout 2 guidelines. Document bugs, no bug report no partial points. tice File Edit View Insert Annotation Workspace Window Help Q 2 IR NIVES SENSE SENWES CA iterations initialvalue filename (A) Implement the HITS algorithm as explained in class/Subject notes adhering to the guidelines of Handout 2. Pay attention to the sequence of update operations and the scaling. For an example of the Subject notes, you have output for various initialization vectors. You need to implement class or function hits (e.g. hitsWXYZ. For an explanation of the arguments see the discussion on PageRank to follow. % java hits iterations initialvalue filename % ./hits (B) Implement Google's PageRank algorithm as explained in class/Subject notes adhering also to the guidelines of Handout 2 and this description. The input for this and the previous) problem would be a file containing a graph represented through an adjacency list representation. The command-line interface is as follows. First we have the class/binary file (eg pork). Next we have an argument that denotes the number of iterations if it is a positive integer or an errorrate for a negative or zero integer value. The next argument initialvalue indicates the common initial values of the vector(s) used. The final argument is a string indicating the filename that stores the input graph. % /perk iteration initialvalue 11lenane // in fact pgrXWXYZ X java perk iterations initialvalue filene // in fact perkWXYZ The two algorithms are iterative. In particular, at iteration tall pagerank values are computed using results from iteration - 1. The initialvalue helps us to set-up the initial values of iteration 0 as needed. Moreover, in PageRank, parameter d would be set to 0.85. The PageRank PR(A) of vertex A depends on the PageRanks of vertices Ti...... incident to A. i.e. pointing to A; check Subject 7 section 3.6 for more details. The pageranks at iteration I use the pageranks of iteration : - 1 (synchronous update). Thus PR(A) on the left in the PageRank equation is for iteration 1, but all PR (T) values are from the previous iteration 1-1. Be careful and synchronize! In order to run the algorithm' we either run it for a fixed number of iterations and iterations determines that, or for a fixed errorrate (an alias for iterations); an iterations equal to 0 corresponds to a default errorrate of 10-5.A-1, -2, etc , -6 for iterations becomes an errorrate of 10-10-2... 10 respectively. At iteration / when all authority/hub/PageRank values have been computed (and auth/hub values scaled) we compare for every vertex the current and the previous iteration values. If the difference is less than errorrate for EVERY VERTEX, then and only then can we stop at iteration 1. Argument initialvalue sets the initial vector values. If it is Othey are initialized to 0, if it is 1 they are initialized to 1. If it is -1 they are initialized to 1/N, where N is the number of web pages (vertices of the graph). If it is -2 they are initialized to 1/VN. filename first.) e Edit View Insert Annotation Workspace Window Help >> comamng a graper represeme unough an aujacency is representation. The command-tme merace is as follows. First we have the class/binary file (eg pgrk). Next we have an argument that denotes the number of iterations if it is a positive integer or an errorrate for a negative or zero integer value. The next argument initialvalue indicates the common initial values of the vector(s) used. The final argument is a string indicating the filename that stores the input graph. %/pgrk iterations initialvalue filename // in fact pgrkwXYZ % java pgrk iterations initialvalue filename // in fact pgr&WXYZ The two algorithms are iterative. In particular, at iteration all pagerank values are computed using results from iteration : - 1. The initialvalue helps us to set-up the initial values of iteration 0 as needed. Moreover, in PageRank, parameter d would be set to 0.85. The PageRank PR(A) of vertex A depends on the PageRanks of vertices Ti....... incident to A, i.e. pointing to A; check Subject 7 section 3.6 for more details. The pageranks at iteration / use the pageranks of iteration - 1 (synchronous update). Thus PR(A) on the left in the PageRank equation is for iteration t, but all PR (T) values are from the previous iteration 1-1. Be careful and synchronize! In order to run the 'algorithm' we either run it for a fixed number of iterations and iterations determines that, or for a fixed errorrate (an alias for iterations); an iterations equal to 0 corresponds to a default errorrate of 10-5 A-1, -2, etc , -6 for iterations becomes an errorrate of 10-10-2,...,10-respectively. At iteration when all authority/hub/PageRank values have been computed (and auth/hub values scaled) we compare for every vertex the current and the previous iteration values. If the difference is less than errorrate for EVERY VERTEX, then and only then can we stop at iteration 1. Argument initialvalue sets the initial vector values. If it is Othey are initialized to 0. if it is 1 they are initialized to 1. If it is -1 they are initialized to 1/N, where N is the number of web-pages (vertices of the graph). If it is -2 they are initialized to 1/VN. filename first.) Argument filename describes the input (directed) graph and it has the following form. The first line contains two numbers: the number of vertices followed by the number of edges which is also the number of remaining lines. PAY ATTENTION THAT NUMBER of VERTICES comes first. The sample graph is treacherous: n and m are the same! All vertices are labeled 0,...,N-1. Expect N to be less than 1,000,000. In each line an edge (ij) is represented by i j. Thus our graph has (directed) edges (0,2),(0,3), (1,0),(2,1). Vector values are printed to 7 decimal digits. If the graph has N GREATER than 10, then the values for iterations, initialvalue are automatically set to O and -1 respectively. In such a case the hub/authority/pageranks at the stopping iteration (i.et) are ONLY shown, one per line. The graph below will be referred to as samplegraph.txt Edit View Insert Annotation Workspace Window Help 44 02 03 10 21 The following invocations relate to samplegraph.txt, with a fixed number of iterations and the fixed error rate that determines how many iterations will run. Your code should compute for this graph the same rank values (intermediate and final). A sample of the output for the case of N > 10 is shown (output truncated to first 4 lines of it). %./perk 15 -1 nasplegraph.txt Base OPC 0] -0.2500000 PE 11-0.2500000 PE 23-0.2500000 PE 3)-0.2500000 Iter # 1 P 0-0.2500000 Pt 1)-0.25000GO P[ 21-0.1437500 Pt 3)-0.1437500 Iter I 2PC 0] -0.2500000 PC 1)-0.1596875 P[ 2] -0.1437500 P 3)-0.1437500 Iter # 3 PI 0)-0.1732344 PL 1)-0.1596875 PC 2) -0.1437500 PE 33-0.1437500 Iter 4 PI 03-0.1732344 PE :)-0.1596875 PT 2)-0.1111246 PE 33-0.1111246 Iter 1 SP 0-0.1732344 PL 1)-0.1319559 Pt 2) -0.1111246 PE 33-0.1111246 Iter 670)-0.1496625 Pt 1)-0.1319559 PC 2-0.1111246 PC 3)-0.1111246 Iter 7 P 0) 0.1496625 PL 1)-0.1319559 PE 2) -0.1011066 PC 3)-0.1011066 Iter 8PCO)-0.1496625 PE 1)-0.1234406 P[ 2] -0.1011066 PE 3)-0.1011066 Iter 19 PI 01-0.1424245 Pt 1)-0.1234406 PC 21-0.1011066 PE 33-0.1011006 Iter 10 PL 03-0.1424245 Pt 1)-0.1234406 PT 2) -0.0980304 PC a)-0.0980304 Iter 11 PE 0] -0.1424245 PC :) -0.1208259 PC 2)-0.0980304 PL 3)-0.0980304 Iter 12 PI 03-01402090 PE 1)-0.1208259 PE 21-0.0980304 PE 3)-0.0980304 Iter : 13 PI 03-0.1402020 PE 11-01208259 PE 21-0.0970858 PC 3)-0.0970858 Iter 14 P[00.1402020 PO 1)-0.1200230 P[ 2) -0,0970858 PC 3)-0.0970858 Iter 15 :P[ 0-0.1395195 PC 1)-0.1200230 PC 23-0.0970858 PC 33-0.0970858 */perk -3 -1 samplegraph.txt Base OP[0] -0.2500000 PC :)-0.2500000 PC 2)-0.2500000 P 3)-0.2500000 Iter # 1 P 0-0.2500000 PC 1)-0.2500000 PE 23-0.1437500 PC 3)-0.1437500 Iter + 2 PE 0-0.2500000 PE 1)-0.1596875 PE 23-0.1437500 PE 33-0.1437500 Iter 3 [0] -0.1732344 Pt 1)-0.1596875 PC 2) -0.1437500 PT 3)-0.1437500 Iter PC)-0.1732344 PL 1)-0.1596875 PL 21-0.1111246 PC 3)-0.1111246 Iter 5 P[ ] 0.1732344 PC )-0.1319559 PC 2)-0.1111246 PC 3)-0.1111246 Iter 6 Pt 03-0.1496625 PE 1)-0.1319559 PE 2)-0.1111246 PE 33-0.1111246 Iter 17 PC 0-0.1496625 Pt 1)-0.1319559 P[ 2] -0.1011006 PC 3)-0.1011066 Iter 18 PE 0.1496625 PC 1)-0.1234406 PC 2)=0.1011066 PC 30.1011066 Iter : 9 :P[0] -0.1424245 PL 1)-0.1234406 PC 2] -0.1011066 PC 3)-0.1011066 Iter 10 PL 03-0.1424245 PE 1)-0.1234406 PC 2-0.0980304 PL 31-0.0980304 Iter 111 Pt 0-0.1424245 PC 1-0.1208259 PT 2) -0.0200304 PE 3-0.0980304 Iter 12 PI 0-0.1402020 P[ 1)-0.1208269 P[ 2] -0.0980304 PE 33-0.0980304 Iter 113 PE 0-0.1402020 PC 11-01208259 PT 2)-0.0970858 PC 3)-0.0070858 % /pgrk 0 -1 verylargegraph.txt Iter P[0] -0.0136364 P[ 1)-0.0194318 P[ 2] -0.0310227 ... other vertices omitted View Insert Annotation Workspace Window Help Iter Iter Iter Iter Iter Iter Iter Iter Iter OLVENDE VOOR EEN FOUVERN 17 PC 0)-0.1496625 PC 1] -0.1319559 Pt 2) -0.1011066 PC 3)-0.1011066 18:P[0] -0.1496625 PC 1] -0.1234406 PC 2) -0.1011066 PC 3)-0.1011066 + 9 P[0] -0.1424245 P[ 1] -0.1234406 PE 2) -0.1011066 PC 3)-0.1011066 10 :P[ 01-0.1424245 PL 11-0. 1234406 PC 21-0.0980304 PL 3)-0.0980304 : 11 :P[0] -0.1424245 PC 1] -0.1206259 Pt 2) -0.0980304 PL 3)-0.0980304 1 12 P[0] -0.1402020 PC 1] -0.1208259 PC 2) -0.0980304 PC 3)-0.0980304 + 13 :P[0)-0.1402020 PC 11-0.1206259 PC 2) -0.0970858 PC 3)-0.0970858 : 14 Pt 0)-0.1402020 PL 1)-0.1200230 PC 21 -0.0970858 PC 3)-0.097c8s 1 15 PC 0)-0.1395195 PC 1] -0.1200230 Pt 2)-0.0970858 PC 3)-0.0970858 Iter Iter % /perk -3 -1 samplegraph.txt Base 1 OP 0)-0.2500000 PE 1) -0.2600000 PC 2-0.2500000 PC 3)-0.2500000 Iter 1 PC 0 -0.2500000 PC 11-0.2500000 PC 2) -0.1437500 PC 3) -0.1437500 2 PC 0 -0.2500000 PC 1-0.1596876 Pt 2)-0.1437600 PT 3)-0.1437500 Iter 3 :P0) 0.1732344 PC 1)-0.1596875 PE 2] -0.1437500 PC 33-0.1437500 + 4 PC 03-0.1732344 PC 1)-0.1696875 Pt 2)=0.1111246 PC 3)-0.1111246 Iter SPE0)-0.1732344 PC 11-0.1319559 PC 2] -0.1111246 PC 3)-0.1111246 Iter : 6P 0) 0.1496625 Pt 1)-0.1319559 PC 2-0.1111246 Pt 3)-0.1111246 Iter : :P[0] -0.1496625 Pt 1)-0.1319559 PC 2)-0.1011066 PC 3)-0.1011066 Iter 8PC0] -0.1496625 Pt 1)-0.1234406 PT 2) -0.1011066 PC 3)-0.1011066 Iter 1 9 PC 0-0. 1424245 PL 11-0. 1234406 PC 21-01011066 PC 3-0.1011066 Iter 110 PC 0-0.1424245 Pt 1)-0.1234406 PT 2)=0.0980304 PC 3)-0.0980304 Iter 11 PC 0-0.1424245 PL 11 -0.1208259 PC 2) -0.0980304 Pt 3)-0.0980304 Iter # 12 PC 0-0.1402020 PC 1)-0.1208259 PC 21-0.0980304 PE 3)-0.0980304 Iter 13:P[ 0-0.1402020 PC 11-0.1206259 PT 2) -0.0970858 PC 3)-0.097085 % /pgrk 0-1 verylargegraph.txt Iter PE0)-0.0136364 PC 1)-0.0194318 P[ 23-0.0310227 ... other vertices omitted For the HITS algorithm, you need to print two values not one. Follow the convention of the Subject notes Base0 :A/H( 0)-0.3333333/0.3333333 A/H[ 11-0.3333333/0.3333333 A/H[ 23-0.3333333/0.3333333 Iter : 1 :N/H[0)-0.0000000/0.8320503 M/H[ 13-0.4472136/0.5547002 A/H[ 23-0.8944272/0.0000000 or for large graphs Iter : 37 A/H[0]=0.0000000/0.0000002 A/HC 1]=0.0000001/0.0000238 A/H[2] =0.0000002/1.0000000 A/H[ 3)-0.0000159/0.0000000 Deliverables. Include source code of all implemented functions or classes in an archive per Handout 2 guidelines. Document bugs; no bug report no partial points