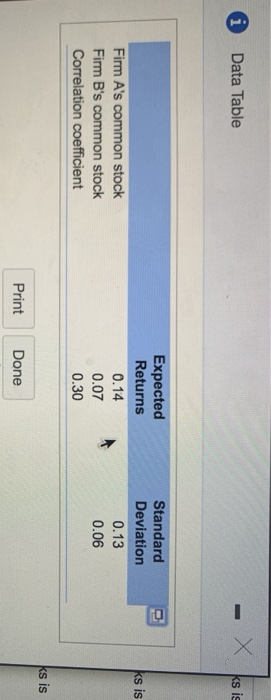
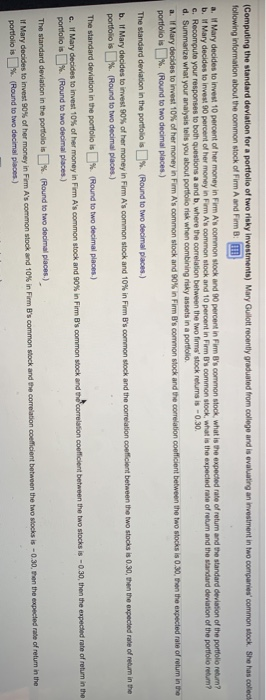
* Data Table X ks is Expected Returns 0.14 Standard Deviation 0.13 ks is Firm A's common stock Firm B's common stock Correlation coefficient 0.07 0.06 0.30 ks is Print Done (Computing the standard deviation for a portfolio of two risky investments) Mary Gullott recently graduated from college and is evaluating an investment in two companies' common stock. She has collect following information about the common stock of Firm A and Firm B 118 a. Mary decides to invest 10 percent of her money in Firm A's common stock and 90 percent in Firm 's common stock, what is the expected rate of return and the standard deviation of the portfolio return? b. Mary decides to invest 90 percent of her money in Form A's common stock and 10 percent in Firm B's common stock, what is the expected rate of return and the standard deviation of the portfolio return? c. Recompute your responses to both questions a and b, where the correlation between the two firms stock returns is -0.30. d. Summarize what your analysis tells you about portioso risk when combining risky assets in a portfolio a. Mary decides to invest 10% of her money in Firm A's common stock and 90% in Firm B's common stock and the correlation coefficient between the two stocks is 0.30, then the expected rate of relum in the portfolio is %. (Round to two decimal places.) The standard deviation in the portfolios % (Round to two decimal places) b. If Mary decides to invest 90% of her money in Firm A's common stock and 10% in Firm B's common stock and the correlation coefficient between the two stocks is 0.30, then the expected rate of return in the portfolio is % (Round to two decimal places.) The standard deviation in the portfolio is % (Round to two decimal places.) 's common stock and the correlation coefficient between the two stocks is -0.30, then the expected rate of return in the Gif Mary decides to invest 10% of her money in Firm A's common stock and 90% in Firm portfolio is 9. (Round to two decimal places.) The standard deviation in the portfolio is % (Round to two decimal places.) if Mary decides to invest 90% of her money in Firm A's common stock and 10% in Firm B's common stock and the correlation coefficient between the two cocks is -0.30, then the expected rate of return in the portfolio is % (Round to two decimal places) Computing the standard deviation for a portfolio of two risky Investments) Mary Guilott recently graduated from college and is evaluating an investment in two companies' common stock. She has cole Following information about the common stock of Firm A and Firm B: a. If Mary decides to invest 10 percent of her money in Firm A's common stock and 90 percent in Firm B's common stock, what is the expected rate of return and the standard deviation of the portfolio return? b. Mary decides to invest 90 percent of her money in Firm A's common stock and 10 percent in Firm 's common stock, what is the expected rate of return and the standard deviation of the portiollo return? c. Recompute your responses to both questions a and b, where the correlation between the two firms' stock returns is - 0.30. d. Summarize what your analysis tells you about portfolio risk when combining risky assets in a portfolio The standard deviation in the portfolio is % (Round to two decimal places) if Mary decides to invest 90% of her money in Firm A's common stock and 10% in Firm B's common stock and the correlation coefficient between the two stocks is -0.30, then the expected rate of return in the portfolio is %. (Round to two decimal places.) The standard deviation of the portfolio is %. (Round to two decimal places.) d. What does your analysis tell you about portfolio risk when combining risk assets in a portfolio? (Select the best choice below) O O A. You can maintain the same return in a portfolio but lower risk if the stocks are positively correlated rather than negatively correlated. Regardless of correlation, risk can also be lowered by investing a higher proportion of the portfolio in stock with higher standard deviation, this however will increase return B . You can maintain the same return in a portfolio but lower risk more if the stocks are negatively correlated rather than positively correlated. If correlation of two stocks is the same, nisk can also be lowered by Investing a higher proportion of the portfolio in stock with lower standard deviation, this however wil effect return C . You can maintain the same return in a portfolio but lower risk the stocks are negatively correlated rather than positively correlated. Regardless of correlation, risk can also be lowered by investing a higher proportion of the portfolio in stock with higher standard deviation, this however will reduce return D . You can maintain the same return in a portfolio but lower risk more if the stocks are positively correlated rather than negatively correlated. If correlation of the two stocks is the same risk can also be lowered by investing a higher proportion of the portfolio in stock with lower standard deviation, this however wil reduce return O O