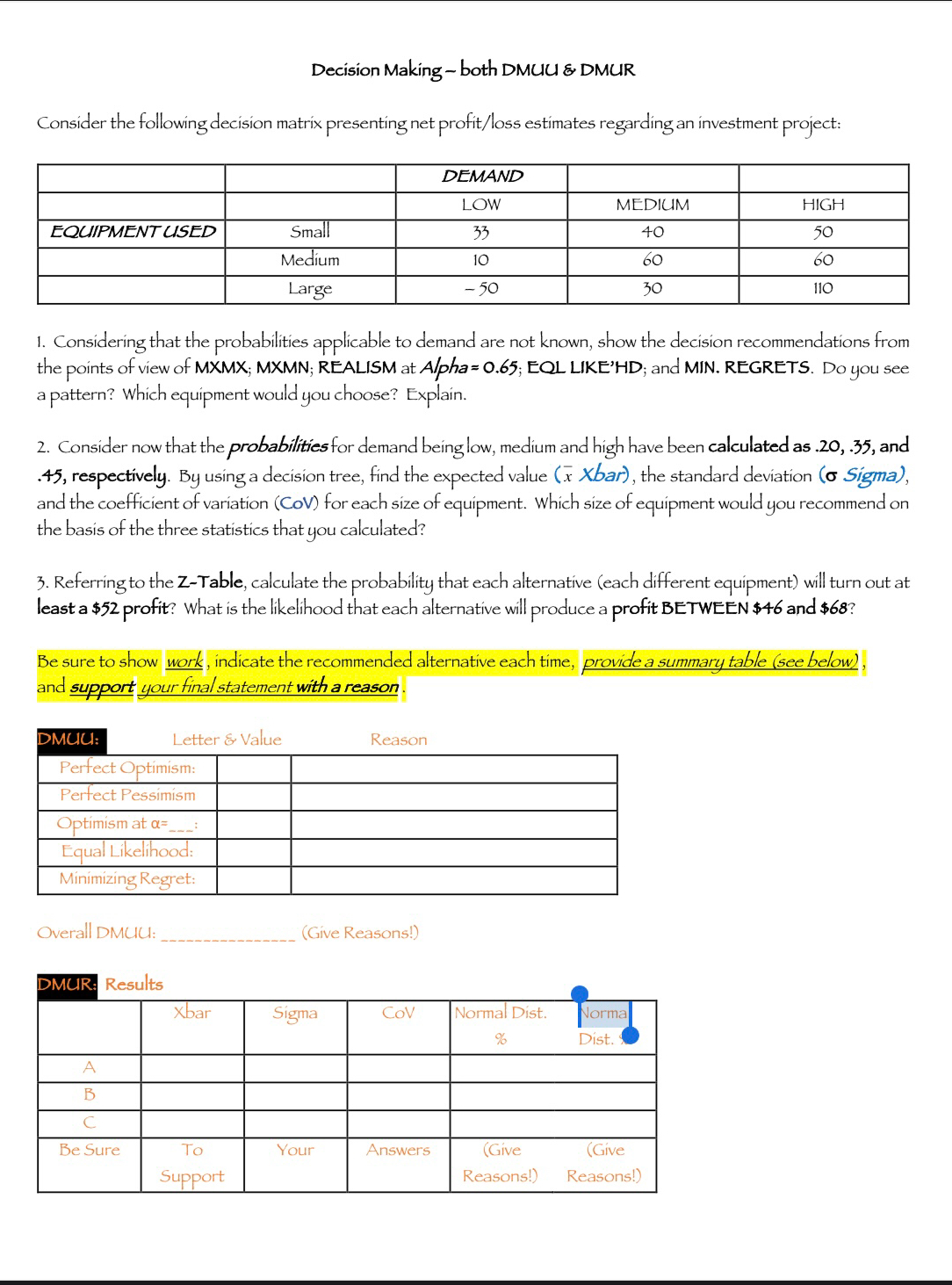
Question: Decision Making - both DMUU & DMUR Consider the following decision matrix presenting net profit / loss estimates regarding an investment project: table [
Decision Making both DMUU & DMUR
Consider the following decision matrix presenting net profitloss estimates regarding an investment project:
tableDEMAND,,LOW,MEDIUM,HIGHEQCIIPMENTUSEDSmall,Medium,Large,
Considering that the probabilities applicable to demand are not known, show the decision recommendations from the points of view of MXMX; MXMN; REALISM at Alpha; EQL LIKE'HD; and MIN. REGRETS. Do you see a pattern? Which equipment would you choose? Explain.
Consider now that the probabilities for demand being low, medium and high have been calculated as and respectively. By using a decision tree, find the expected value Xbar the standard deviation Sigma and the coefficient of variation CoV for each size of equipment. Which size of equipment would you recommend on the basis of the three statistics that you calculated?
Referring to the ZTable, calculate the probability that each alternative each different equipment will turn out at least a $ profit? What is the likelihood that each alternative will produce a profit BETWEEN $ and $
Be sure to show work, indicate the recommended alternative each time, provide a summary table see below and support your final statement with a reason.
tableDMCI:ReasonPerfect Optimism:,Perfect Pessimism,Optimism at Equal Likelihood:,Minimizing Regret:,
Overall DMUU:
Give Reasons!
tableXbar,Sigma,CoV,tableNormal Dist.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


