Question: def add _ edge _ to _ graph ( unique _ weights, edge _ weight ) : if edge _ weight not in unique _
def addedgetographuniqueweights, edgeweight:
if edgeweight not in uniqueweights:
uniqueweights.addedgeweight
return True
return False
def assignlabelsn k:
# initialize an empty list to store vertex labels
vertexlabels
# initialize an empty list to store edge weights
edgeweights
# create a set to store unique edge weights
uniqueweights set
# get the order of sn
orderofsn n
# create a list of integers from to k
labels listrangek
# assign labels to vertices
for i in rangeorderofsn:
vertexlabels.appendlabelsi k
# assign weights to edges
for i in rangeorderofsn:
# Ensure only adjacent vertices are connected
if i orderofsn:
edgeweight absvertexlabelsi vertexlabelsi
if addedgetographuniqueweights, edgeweight:
edgeweights.appendedgeweight
else:
# Adjust vertex labels if edge weight is not unique
vertexlabelsivertexlabelsi k
vertexlabelsi vertexlabelsi k
edgeweights.appendedgeweight
# return the vertex labels and edge weights
return vertexlabels, edgeweights
# Take input for n from the user
n intinputEnter the value of n:
k n # calculate k based on n
vertexlabels, edgeweights assignlabelsn k
printvertex labels:", vertexlabels
printedge weights:", edgeweights
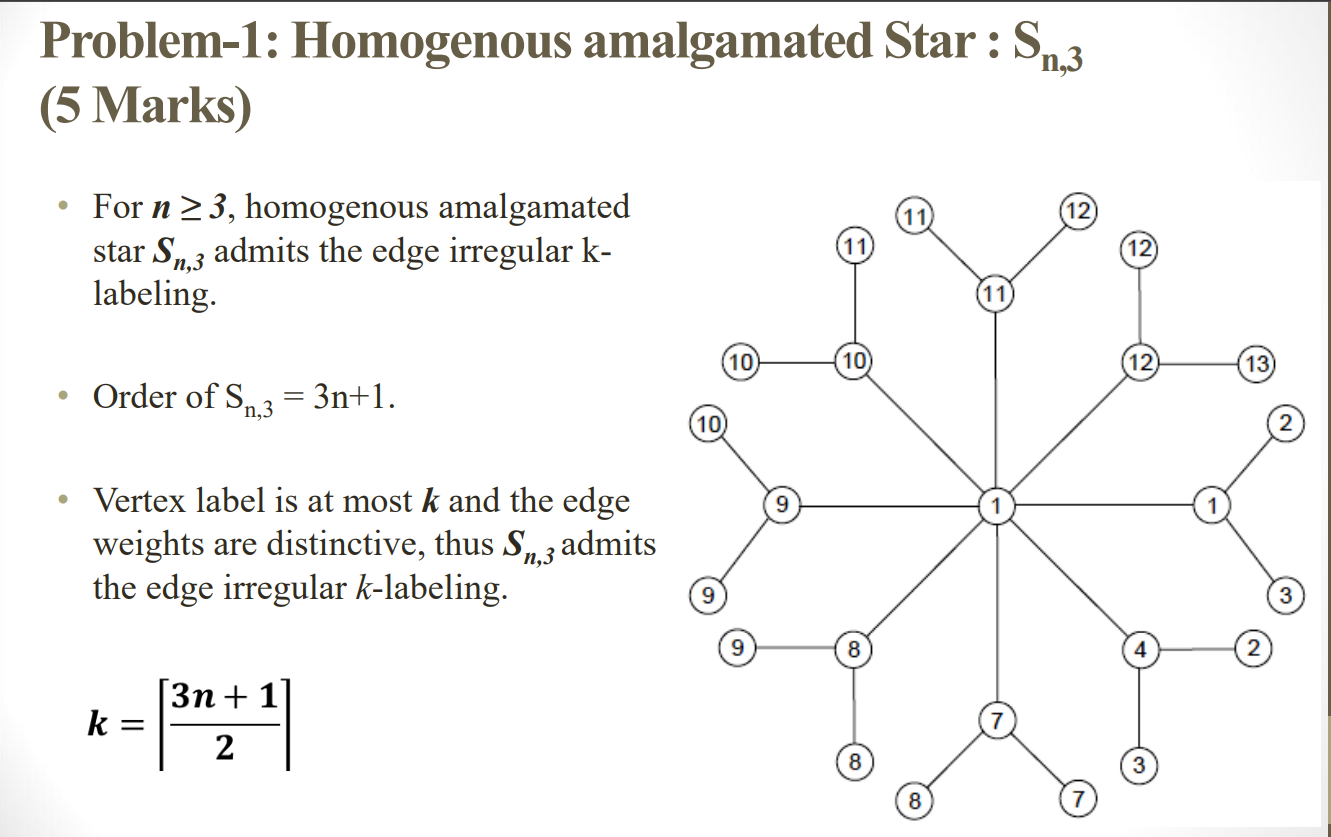
Problem: Homogenous amalgamated Star :
For homogenous amalgamated
star admits the edge irregular k
labeling.
Order of
Vertex label is at most and the edge
weights are distinctive, thus admits
the edge irregular labeling.
~~
Make changes to the above code so that the edge weights should be unique and the output graph should look like the graph provided from the snapshot.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


