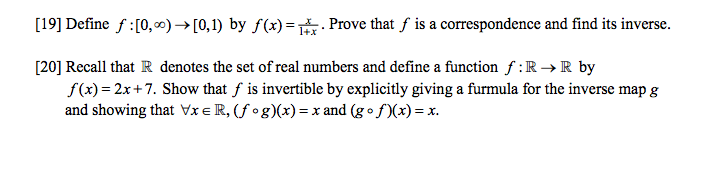
Define f: [0, infinity) rightarrow [0, 1) by f(x) = x/1 + x. Prove that f is a correspondence and find its inverse. Recall that R denotes the set of real numbers and define a function f: R rightarrow R by f(x) = 2x + 7. Show that f is invertible by explicitly giving a furmula for the inverse map g and showing that x R, (f g) (x) = x and (g f) (x) = x. Define f: [0, infinity) rightarrow [0, 1) by f(x) = x/1 + x. Prove that f is a correspondence and find its inverse. Recall that R denotes the set of real numbers and define a function f: R rightarrow R by f(x) = 2x + 7. Show that f is invertible by explicitly giving a furmula for the inverse map g and showing that x R, (f g) (x) = x and (g f) (x) = x