Question: Define f on R ^ ( 2 ) by f ( 0 , 0 ) = 0 , and f ( s , t )
Define f on R by f and
fstststst
for st Show that f is of class C in R and that the mixed
partial derivatives DDf and DDf exist at every point of R but that
DDfDDf PLEASE PROVIDE A COMPELTE AND RIGOROUS ARGUMENT. INCORRECT SOLUTIONS WILL BE DOWNVOTED
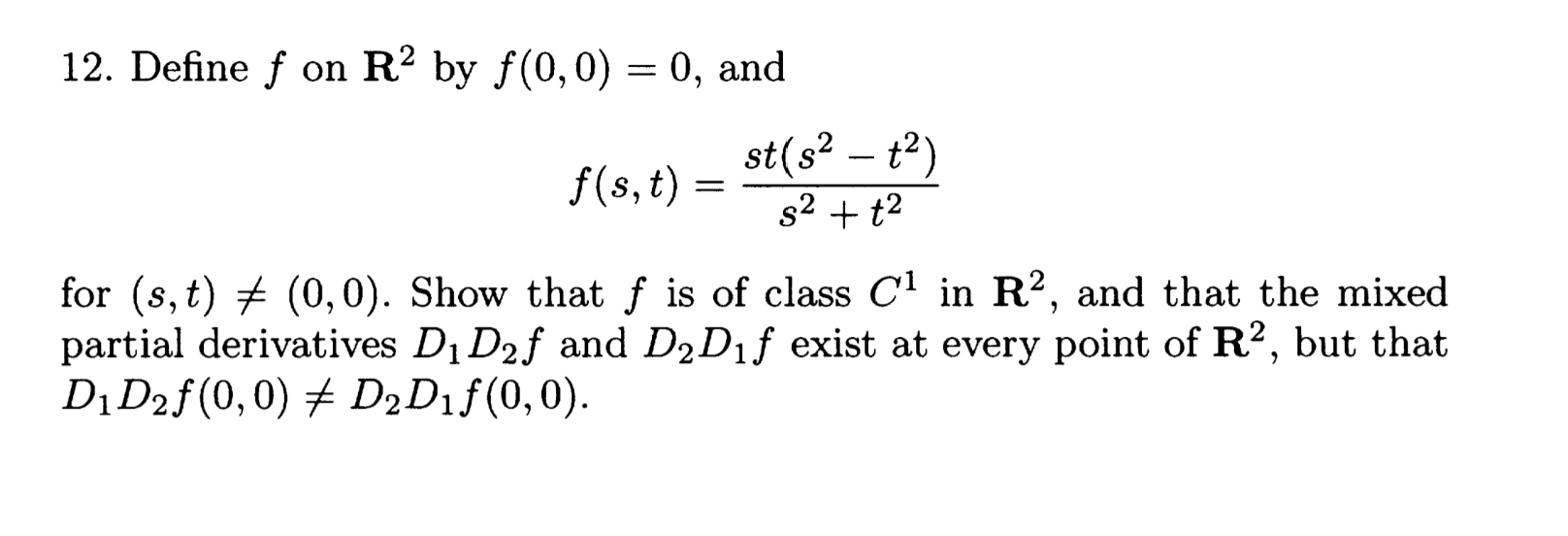
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


