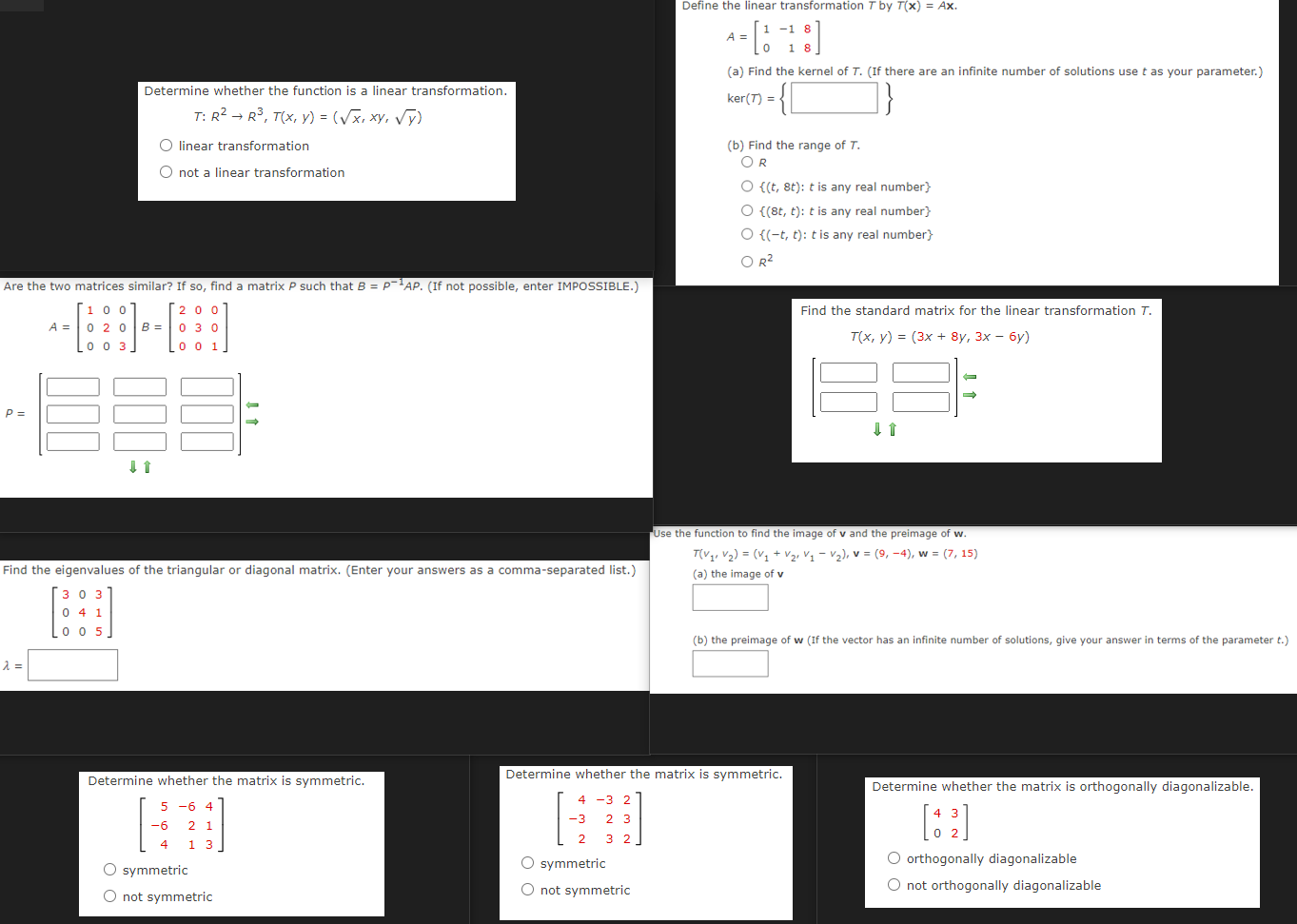
Define the linear transformation T by T(x) = Ax. 4 = 1 48] (a) Find the kernel of T. (If there are an infinite number of solutions use t as your parameter.) Determine whether the function is a linear transformation. ker ( 7) = T: R2 - RS , T ( x, y ) = ( V x, xy, Vy) O linear transformation (b) Find the range of T. OR O not a linear transformation O {(t, 8t): t is any real number} O { (8t, t): t is any real number} O {(-t, t): t is any real number} OR 2 Are the two matrices similar? If so, find a matrix P such that B = PAP. (If not possible, enter IMPOSSIBLE.) Find the standard matrix for the linear transformation . 4 = 020 8 = 03 0 T(x, y) = (3x + 8y, 3x - 6y) J 1 1 1 Use the function to find the image of v and the preimage of w. T(V1 . V2) = (V1 + V2. V1 - V2), V= (9, -4), w = (7, 15) Find the eigenvalues of the triangular or diagonal matrix. (Enter your answers as a comma-separated list.) (a) the image of v 303 041 0 05 (b) the preimage of w (If the vector has an infinite number of solutions, give your answer in terms of the parameter t.) Determine whether the matrix is symmetric. Determine whether the matrix is symmetric. Determine whether the matrix is orthogonally diagonalizable. [: 2] O symmetric O orthogonally diagonalizable O symmetric O not orthogonally diagonalizable not symmetric O not symmetric