Question: Define the Manhattan distance between two points A(Ax, Ay) and B(Bx, By) in a two dimensional space as |Ax Bx|+|Ay By|, denoted by d(A, B).

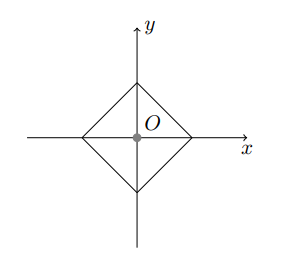
Define the Manhattan distance between two points

Define the Manhattan distance between two points A(Ax, Ay) and B(Bx, By) in a two dimensional space as |Ax Bx|+|Ay By|, denoted by d(A, B). A point is chosen uniformly at random inside a square with each side of length 2. The vertices of the square are on the x or y axis and the centre of the square is at the origin (see the figure below). Let L be the Manhattan distance from the point to the centre of the square (the origin O).

1. What is the CDF of L? 2. What is the PDF of L? 3. What is expected value of L? 4. What is the variance of L?

y T C

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related General Management Questions!

i need help with these, thank you so much 2.1 & Right-handed, orthogonal, unit vectors. (Section 4.1) Draw a set of right-handed orthogonal (mutually perpendicular) unit vectors consisting of Ix, ny,...

Math 636 Final - Quiz Component 1. The system of linear equations 2x2 x3 = 3 2x1 + x2 + 2x3 = 1 x1 + x2 + 3x3 = 2 (a) is consistent with a unique solution. (b) is consistent with infinitely many...

Please answer all the required questions in detail I hope the answer is not copy-paste I hope that the answer will be according to the concepts in the chapter 3 The following article summarizes the...

1 Dimensions and Units 1.1 Physical Dimensions and Units of Measurement You've probably heard the expression that you can't compare apples and oranges. To a physicist, the key concept underlying this...

lup ] (d) Show how a generating (or "mother") wavelet (x) can spawn a family of "daughter" wavelets jk(x) by simple shifting and scaling operations, and explain the advantages of representing...

The experimental result differs from the assumption. The result shows that the ring oscillator frequencies can be grouped into two groups, where the first group is the high frequency group for the...

MATHEMATICS FOR MACHINE LEARNING Marc Peter Deisenroth A. Aldo Faisal Cheng Soon Ong Contents Foreword 1 Part I Mathematical Foundations 9 1 Introduction and Motivation 11 1.1 Finding Words for...

A. B. A. B. ( ( ) ) Beginning and Intermediate Algebra An open source (CC-BY) textbook Available for free download at: http://wallace.ccfaculty.org/book/book.html by Tyler Wallace 1 ISBN...

1 2.3 Definition of a Discrete Probability Function Definition: Let S be a discrete sample space from some experiment. A function P, defined on all events in S, is said to be a probability function...

854 CHAPTER 15 DIFFERENTIATION IN SEVERAL VARIABLES 9. 20. Jessica and I at 2 oh ; h (x , y ) = -, x = 1/2, y = 1712 paths that make a with velocity va 10. "J : f ( x , y , Z ) = xy - 22, x = rcos0,...

Marcia Wilson owns and operates Marcias Dry Cleaning, which is an upscale dry cleaner in a well-to-do suburban neighborhood. Marcia makes her business stand out from the competition by providing...

r Write stack algorithm and apply any example to give the output of each methods "push(b) pop(),size(), isEmpty(), top()" using array or linked list? Then find a minimum number that insert? 2- Write...

Question 2 7 ( 9 polnt ) surneyr Farter 3 it in AA The mannerin which FDIC deposit insurance is set up in the United states encourages banks to reject some loans that probably would be profitable....

Read the articles on journaling and review the template provided. Identify what approach, to journaling, in the articles you found useful and why. Post to the discussion forum that you have reviewed...