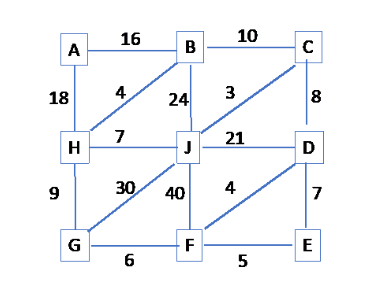
Question: Definition 1 ( Travelling Salesperson Problem ) . Given a list of cities and the distances ( edges ) between each pair of cities (
Definition Travelling Salesperson Problem Given a list of cities and the distances edges between each pair of cities nodes what is the optimal route that visits each city exactly once starting from city A and ending at any other city? AHGFJCDEB Personalize this homework for yourself: Take the last digits of your M# and call is a : Find Namod which will be a number between and : Find Namod which will be a number between and For example: Let a Then Nmod and Nmod Now update the above given citidistances graph by setting the distance of AB to be N and the distance of AH to be N Now, with your personalized graph of cities, answer the following questions: In the search tree, let frontier denote the list that contains all the discovered but unexpanded nodes. pts Perform uniformcost search for the above problem formulation. Show all the changes on frontier until a node containing a fourcity partial tour is pulled out of the list. Each entry in frontier contains the partial tour and its gx value. pts Perform A search for the above problem formulation using hx as the heuristic function. a pts Show all the changes on frontier until a node containing a fourcity partial tour is pulled out from the list. Each entry in frontier contains the partial tour and its fxrho xhx values. b pts Only for the two states AB and AH show the subgraphs and its MCSTsc pts Show the search tree of this time step, ie when a first nodethat contains a fourcity partial tour is pulled out from frointer to expand. pts Perform A search for the above problem formulation using hx as the heuristic function. a pts Show all the changes on frontier until a node containing a fourcity partial tour is pulled out from the list. Each entry in frontier contains the partial tour and its fxgxhx values. b pts Show the search tree of this time step. pts Are hx and hx admissible heuristic functions? Give precise and succinct reasons to justify your answers.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


