Question: Definition: Let R be a relation on the set A. The powers R n n = 1, 2, 3, ... are defined recursively by R1

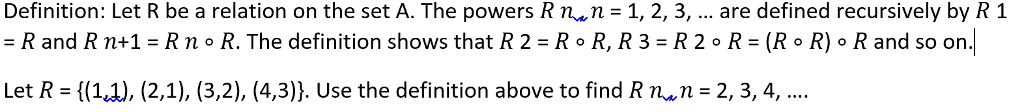
Definition: Let R be a relation on the set A. The

Definition: Let R be a relation on the set A. The powers R n n = 1, 2, 3, ... are defined recursively by R1 = R and R n + 1 = R n compositefunction R. The definition shows that R2 = R compositefunction R, R3 = R2 compositefunction R = (R compositefunction R) compositefunction R and so on. Let R = {(1, 1), (2, 1), (3, 2), (4, 3)}. Use the definition above to find R n n = 2, 3, 4

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

1. (10 Points) Draw the graph represented by each adjacenty matrix with vertices a, b, c, d, e 0101 1 10101 A = 01201 0 0 0 02 1 1 1202. (10 Points) Draw the graph represented by the incidence matrix...

This Journal entry has two parts: Part A: Select TWO examples of solutions to trig identities from the Content section ( Examples or Check your Understanding ) or from Assignment 1 Solutions....

and confidence in solving math problems. Seek help when needed: If you are struggling to solve a math problem, don't be afraid to seek help. Talk to your teacher or a tutor, or join a study group to...

from your peers. There are also many online resources and forums where you can ask questions and get help from experts in the field. DO ENTIRE QUESTIONs Read the problem carefully: Before you start...

a math problem, don't be afraid to seek help. Talk to your teacher or a tutor, or join a study group to get help from your peers. There are also many online resources and forums where you can ask...

answer. This not only helps you keep track of your progress, but also makes it easier to check your work and identify any mistakes you may have made. DO ENTIRE QUESTIONs Read the problem carefully:...

important to show your work. Write down each step of the solution and show how you arrived at your answer. This not only helps you keep track of your progress, but also makes it easier to check your...

u arrived at your answer. This not only helps you keep track of your progress, but also makes it easier to check your work and identify any mistakes you may have made. DO ENTIRE QUESTIONs Read the...

take, don't get discouraged. Instead, use it as an opportunity to learn and improve your problem-solving skills.Break the problem down into smaller parts. If you are struggling to solve a problem,...

a graph. Vectors can be added and subtracted, and the resulting vector is called the DO ENTIRE QUESTIONs Read the problem carefully: Before you start solving the problem, make sure you understand...

Lane Company manufactures a single product and applies overhead cost to that product using standard direct labor-hours. The budgeted variable manufacturing overhead is $4.00 per direct labor-hour and...

4) Assume that the database block size is 2K. Also assume that the Oracle database uses PCTFREE 20 percent and PCTUSED 40 percent. For this problem we will assume that any overhead in blocks is zero....

E13.16 (LO 1, 3) (Entries for Retirement and Issuance of Bonds) Kobiachi Group had bonds outstanding with a maturity value of 5,000,000. On April 30, 2026, when these bonds had an unamortized...

4 . 4 JOJO Ltd is a clothing retailer and need to calculate the selling price for a new jumper. Here are the costs involved in producing a single jumper: Raw Materials: R 1 0 Labour Costs: R 2 0...

LO3 Outline strategic compensation decisions.

LO5 Discuss the importance of training managers and employees on performance appraisal and give examples of rater errors.

LO4 Describe the advantages and disadvantages of multisource (360-degree) appraisals.