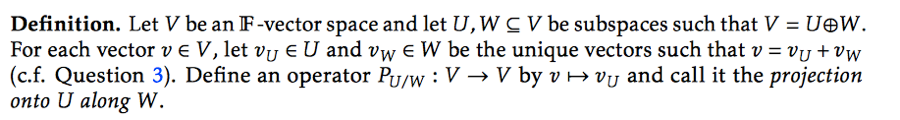
Definition. Let V be an IF-vector space and let U, W C V be subspaces such that V = UeW. For each vector ve V, let vy E U and vw E W be the unique vectors such that v = vu + vw (c.f. Question 3). Define an operator Pu/w : V - V by v - vy and call it the projection onto U along W.5. V be an IF-vector space and let U, W C V be subspaces such that V = Ue W. Prove: (a) Pu/w is a linear operator. (b) ker(Pu/w) = W and im(Pu/w) = U. (c) Pu/wly = idy, where recall that Pu/wly denotes the restriction of the function Pu/w to the set U. (d) Pu/w is idempotent, i.e. Pu/w = Pu/w, where Pu/w = PU/W . PU/W