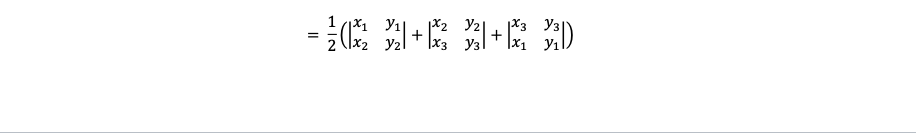
Definition (Simple Polygon): A polygon that does not intersect itself and has no holes. In Video 7 we developed the shoelace formula (or shoelace algorithm or Gauss's area formula or surveyor's formula) for a special simple polygon - a triangle (n = 3). In this problem we will generalize this formula for a simple polygon with n vertices. The formula is represented by: Area = 7 (x2 yz + X2 12 X3 )3| 1+ (x3 13 x4 yal [*n-1 yn-1| [Xn Vn) *n where (x1, yi), i = 1,2, ., n are the vertices of the simple polygon labeled sequentially in the counterclockwise direction. We want to prove the formula above is true for all n 2 3 using the Principle of Mathematical Induction. First step: Show the formula is true for n = 3 (a triangle). We did this in Video 7 by showing a triangle with vertices (x, , y,), (X2 , y2) , and (X; , ), ) has Area = = (X1)2 - X2)1 + X2)3 - X3)/2 + X3)1 - X1)3)\fAlthough it is not necessary, often it is useful (or helpful) to look at the next iteration (in this case n = 4) to get an idea of how it relates to the previous situation (n = 3). We will do that at this time by considering a simple polygon with four vertices (x1, y1), (x2, y2), (x3, V3) and (x4, 14) mapped counterclockwise around the polygon. Following the same algorithm, we used Video 7, we get Area = (x1)2 - X2)1 + X2)/3 - X3)/2 + X3)/4 -X4V/3 + X4)1 - X1y4) yal + x, vil). You may want to revisit the relationship between n = 3 and n = 4 by drawing a picture as you move forward with the rest of the proof. Problem: (this is the part you complete) Second step (the induction step): Prove that If the result is true for n = k, (In other words, assume the area of a simple polygon with no = k vertices is then the result is true for n = k + 1. (Draw a picture!)