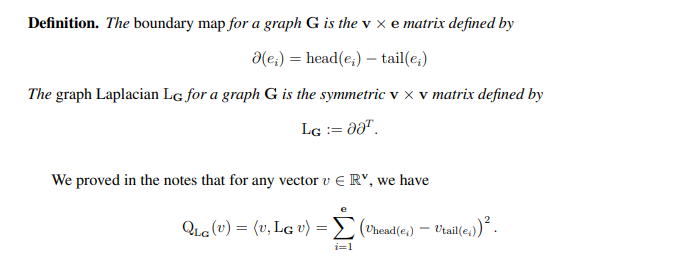
Definition. The boundary map for a graph G is the v x e matrix defined by ale;) = head(ei) taille:) The graph Laplacian LG for a graph G is the symmetric v x v matrix defined by LG := ao We proved in the notes that for any vector v E RY, we have QLc (u) = (v, LG v) = (head(e) Vtaille.) (e)). i=1 3. (10 points) Let I1 <... be the eigenvalues of symmetric matrix lg. points prove that by finding a vector v e ry so lg definition. set s vertices g is called component if there are no edges join- ing in to outside s. largest disjoint components connected g. has d then ...="\d" hint: really partition into separate graphs g1 gd. boundary map for graph x defined ale head taille: laplacian :="ao" we proved notes any have qlc vtaille. i="1" let i1 gd>