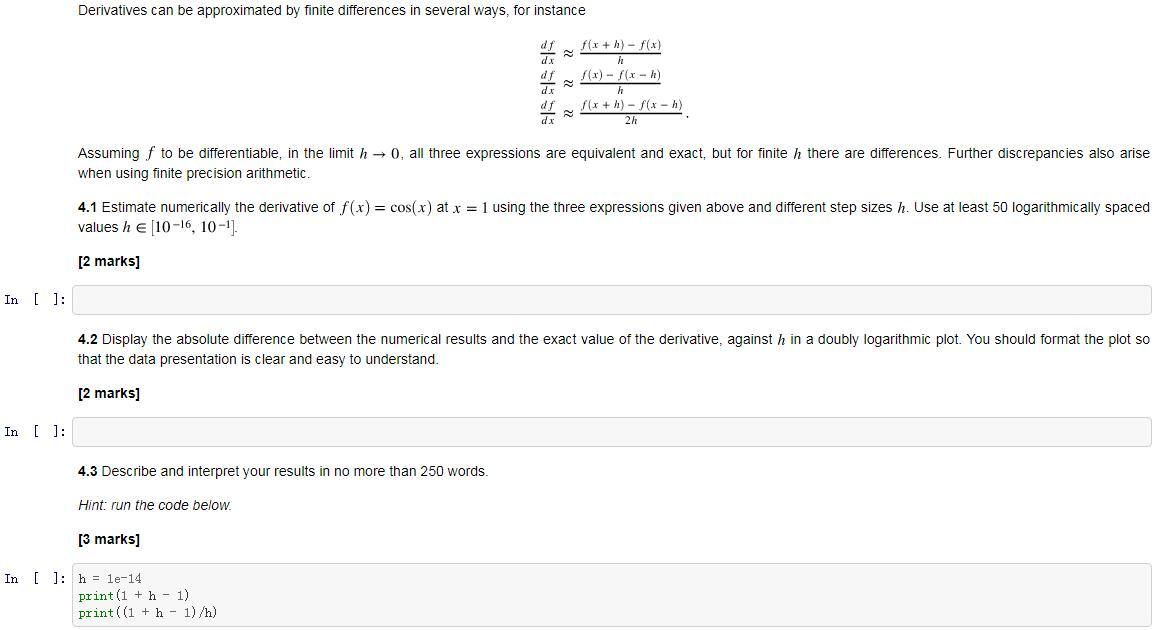
Derivatives can be approximated by finite differences in several ways, for instance dx 2 2 2 f(x + h) - f(x - h) 2h Assuming f to be differentiable, in the limit h0, all three expressions are equivalent and exact, but for finite h there are differences. Further discrepancies also arise when using finite precision arithmetic. 4.1 Estimate numerically the derivative of f(x) = cos(x) at x = 1 using the three expressions given above and different step sizes h. Use at least 50 logarithmically spaced values h [10-16, 10-1]. [2 marks] In [ ]: 4.2 Display the absolute difference between the numerical results and the exact value of the derivative, against h in a doubly logarithmic plot. You should format the plot so that the data presentation is clear and easy to understand. [2 marks] In [ [ ]: 4.3 Describe and interpret your results in no more than 250 words. Hint: run the code below. [3 marks] In [ ]: h = le-14 print (1 + h - 1) print((1 + h - 1) /h) Derivatives can be approximated by finite differences in several ways, for instance dx 2 2 2 f(x + h) - f(x - h) 2h Assuming f to be differentiable, in the limit h0, all three expressions are equivalent and exact, but for finite h there are differences. Further discrepancies also arise when using finite precision arithmetic. 4.1 Estimate numerically the derivative of f(x) = cos(x) at x = 1 using the three expressions given above and different step sizes h. Use at least 50 logarithmically spaced values h [10-16, 10-1]. [2 marks] In [ ]: 4.2 Display the absolute difference between the numerical results and the exact value of the derivative, against h in a doubly logarithmic plot. You should format the plot so that the data presentation is clear and easy to understand. [2 marks] In [ [ ]: 4.3 Describe and interpret your results in no more than 250 words. Hint: run the code below. [3 marks] In [ ]: h = le-14 print (1 + h - 1) print((1 + h - 1) /h)