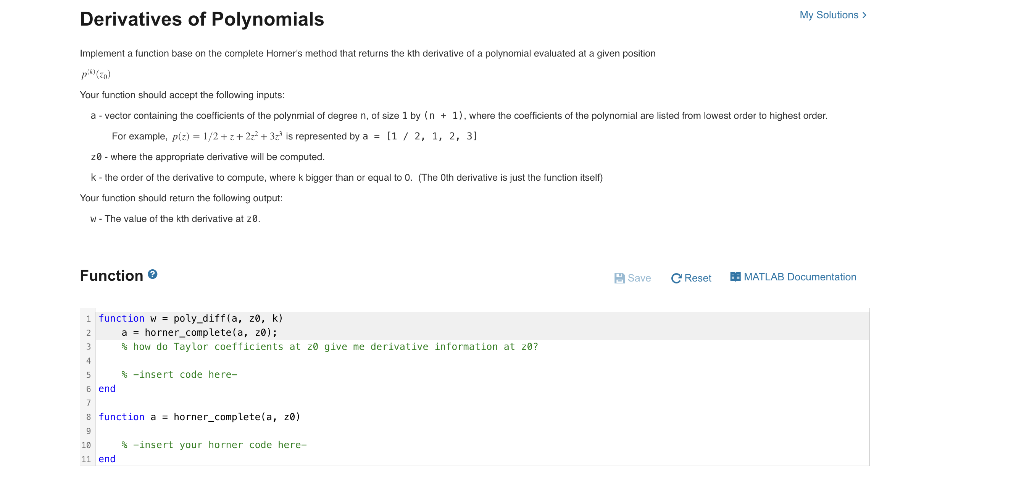
Derivatives of Polynomials Implement a function base on the complete Homer's method that returns the kth derivative of a polynomial evaluated at a given position p(6)(0) Your function should accept the following inputs: a - vector containing the coefficients of the polynmial of degree n, of size 1 by (n+1), where the coefficients of the polynomial are listed from lowest order to highest order. For example, p(z)=1/2+z+2z2+3z3 is represented by a=[1/2,1,2,3] 20 - where the appropriate derivative will be computed. k - the order of the derivative to compute, where k bigger than or equal to 0 . (The oth derivalive is just the function itself) Your function should return the following output: w - The value of the kth derivative at 20 . Function