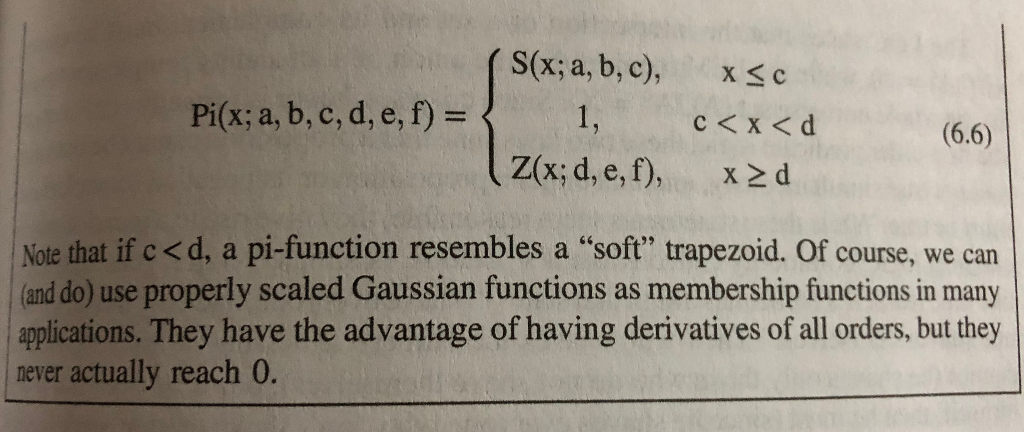
Derive the equation for the S-function of Example 6.1. Hint: There are two parabola pieces and for each piece you know two points, the value of the function at two of the parameters. But wait you say, a parabola has three coefficients, so you need at least three equations to find them. Think about the derivative. 6.3. A. B. Show that a symmetric S-function (where b is the midpoint of a and c) has a well-defined derivative at all points in its domain (even at the "join" points). Let X Pi(x; 1,2,3,3,4,5), and Pi(x; 4,5,6,7,8, 10). C. [0, 10]. Define and graph the functions S(x; 5,7,9), Z(x; 2,3,6), Derive the equation for the S-function of Example 6.1. Hint: There are two parabola pieces and for each piece you know two points, the value of the function at two of the parameters. But wait you say, a parabola has three coefficients, so you need at least three equations to find them. Think about the derivative. 6.3. A. B. Show that a symmetric S-function (where b is the midpoint of a and c) has a well-defined derivative at all points in its domain (even at the "join" points). Let X Pi(x; 1,2,3,3,4,5), and Pi(x; 4,5,6,7,8, 10). C. [0, 10]. Define and graph the functions S(x; 5,7,9), Z(x; 2,3,6)