Question: Derive the total, average and marginal long run cost functions for the production function: Question 7: Derive the total, average and marginal long run cost

Derive the total, average and marginal long run cost functions for the production function:

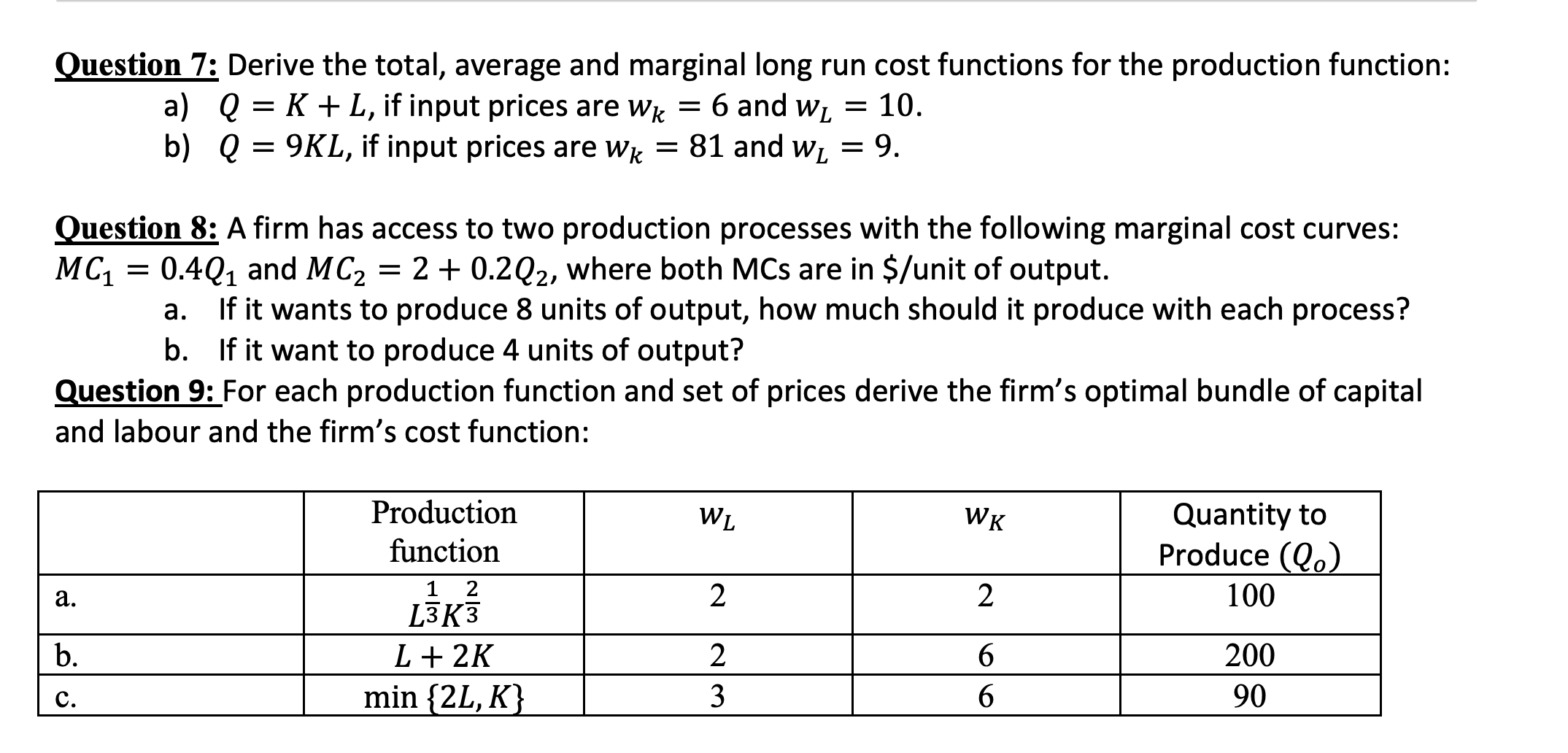
Question 7: Derive the total, average and marginal long run cost functions for the production function: a) Q = K + L, if input prices are Wk = 6 and WL = 10. b) Q = 9KL, if input prices are Wk = 81 and WL = 9. Question 8: A firm has access to two production processes with the following marginal cost curves: MC1 = 0.4Q1 and MC2 = 2 + 0.2Q2, where both MCs are in $/unit of output. a. If it wants to produce 8 units of output, how much should it produce with each process? b. If it want to produce 4 units of output? Question 9: For each production function and set of prices derive the firm's optimal bundle of capital and labour and the firm's cost function: Production WL WK Quantity to function Produce (Qo) a. 1 2 L3K 3 2 2 100 b. L + 2K 2 6 200 C. min {2L, K} 3 6 90

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Economics Questions!

a) Production functions show the highest output that a firm can produce for every specified combination of inputs, but why do we distinguish between short run and long run production functions?...

A firm producing hockey sticks has a production function given by Take a firm with production function q = 2vkl. Assume the firm cannot vary its capital in the short run, and that k=100. Also assume...

Question 1. [Utility Maximization and Choice] Tom's utility on two goods, and , is presented as below. utility = (, ) = a) ( 10 points ) If x costs $1 each and y costs $2 each, determine his...

Not yet answered Question 2 Marked out of 50.00 Consider the demand schedule for pizzas produced by a perfect competitor In Table 2. Assume that the price of pizzas is $12.50 P Fing question Table 2:...

A: Suppose you have a homothetic production technology and you face input prices (w,r). (a) On a graph with labor on the horizontal and capital k on the vertical axis, illustrate a ray along which...

Need help with this question. thank you A firm produces cellphones (y) with two factors of production: labor (l) and capital (k). Its technology is represented by the production functiony=lk 2 . (a)...

3. A firm produces iPhones (y) with two factors of production: labor (1) and capital (k). Its technology is represented by the production function y = 1k2. (a) Represent graphically the isoquants of...

A government wants to reduce electricity consumption by 10%. The price elasticity of demand for electricity is 0.1. The government must __________ the price of electricity by __________. A. raise; 1%...

A: Suppose the production process for a firm is homothetic and has decreasing returns to scale. (a) On a graph with labor on the horizontal and capital k on the vertical axis, draw an isoquant...

ng isocosts and isoquants, you were able to obtain the optimal cost for a firm to produce iven level of output. a) Based on this, we can now derive various cost functions for a given level of output....

Explain the differences among CPMs, TCPMs, and CPPs. How are they used to estimate the cost efficiency of a media plan?

a. What journal entries should the county make in July 2018 to record the in-substance defeasance of the 1998 debt in its debt service fund? b. What debt should be reported in the countys...

S&P 5 0 0 Microsoft Close 1 2 / 3 1 / 2 0 0 9 1 1 1 5 . 1 0 3 0 . 4 8 0 9 / 3 0 / 2 0 0 9 1 0 5 7 . 0 8 2 5 . 5 5 0 6 / 3 0 / 2 0 0 9 9 1 9 . 3 2 2 3 . 3 5 0 3 / 3 0 / 2 0 0 9 7 9 7 . 8 7 1 8 . 1 3 1...

Chandler Tire Co. is trying to decide which one of two projects it should accept. Both projects have the same start-up costs. Project 1 will produce annual cash flows of $56,000 a year for 6 years....

4. How does the problem of limited and bundled choice in the public sector relate to economic efficiency? Why are public bureaucracies possibly less efficient than business firms? LO5.2

5. Discuss the political incentives that helped motivate federal politicians to approve budget deficits in all but five years between 1960 and 2015. LO5.2

2. We can apply voting paradoxes to the highway construction example of Chapter 4. Suppose there are only five people in a society and each favors one of the five highway construction options listed...