Descrete Probability

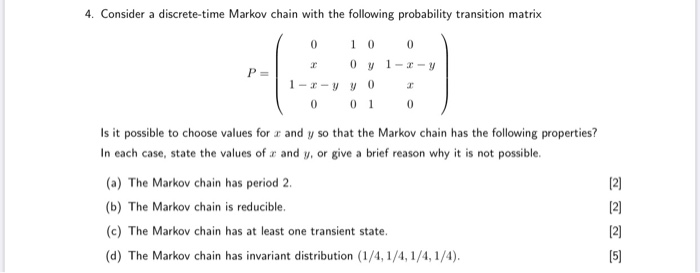
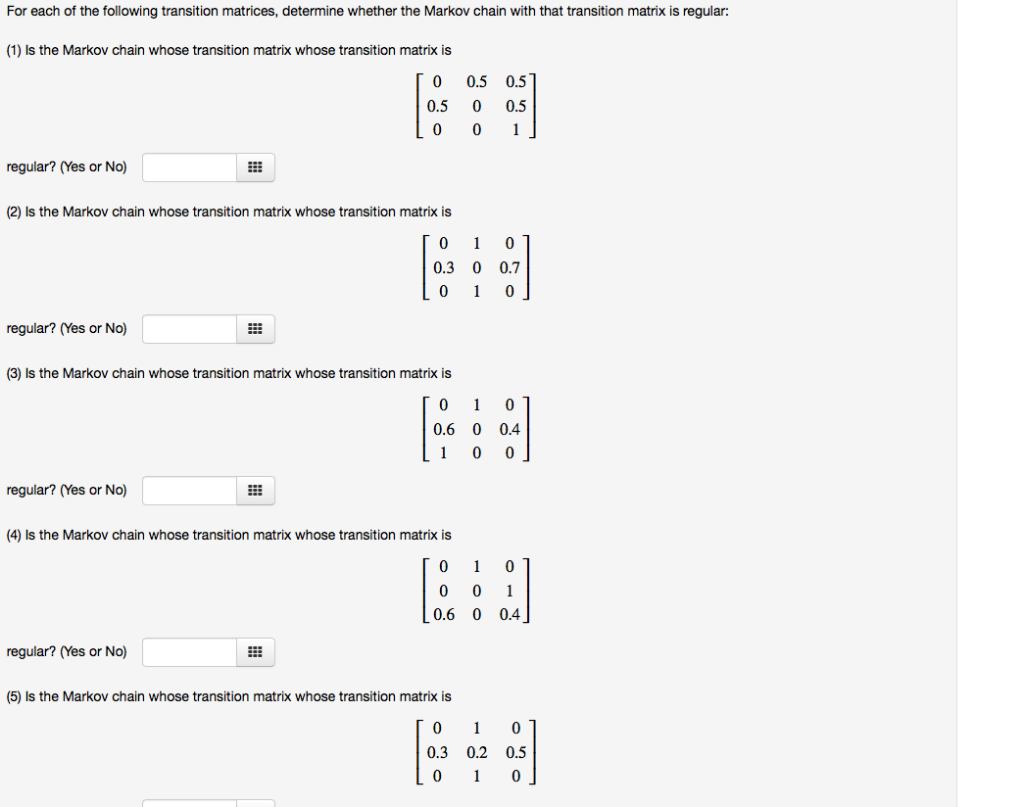
4. Consider a discrete-time Markov chain with the following probability transition matrix 0 0 0 0 7 1-3-y P = 1-I-VVO T 0 0 1 0 Is it possible to choose values for a and y so that the Markov chain has the following properties? In each case, state the values of a and y, or give a brief reason why it is not possible. (a) The Markov chain has period 2. [2) (b) The Markov chain is reducible. (c) The Markov chain has at least one transient state. UNN (d) The Markov chain has invariant distribution (1/4, 1/4, 1/4, 1/4).For each of the following transition matrices, determine whether the Markov chain with that transition matrix is regular: (1) Is the Markov chain whose transition matrix whose transition matrix is 0 0.5 0.5 0.5 0 0.5 0 0 regular? (Yes or No) (2) Is the Markov chain whose transition matrix whose transition matrix is 0 1 0 0.3 0 0.7 0 0 regular? (Yes or No) (3) Is the Markov chain whose transition matrix whose transition matrix is 0 1 0 0.6 0 0.4 1 0 0 regular? (Yes or No) (4) Is the Markov chain whose transition matrix whose transition matrix is 0 1 0 0 0.6 0 0.4 regular? (Yes or No) (5) Is the Markov chain whose transition matrix whose transition matrix is 0 1 0 0.3 0.2 0.5 0 1 0For each of the following transition matrices, determine whether the Markov chain with that transition matrix is regular: (1) Is the Markov chain whose transition matrix whose transition matrix is 1 0.2 0.8 0 0 regular? (Yes or No) (2) Is the Markov chain whose transition matrix whose transition matrix is 0 1 0.1 0.4 0.5 0 1 regular? (Yes or No) (3) Is the Markov chain whose transition matrix whose transition matrix is 0 0 0.8 0 0.2 0.8 0.2 0 regular? (Yes or No) (4) Is the Markov chain whose transition matrix whose transition matrix is 0 1 0.8 0 0.2 0 1 0 regular? (Yes or No)1. Consider the Markov chain with state space {0, 1, 2} and transition matrix 1 2 P = HO 2 (a) Suppose Xo = 0. Find the probability that X2 = 2. (b) Find the stationary distribution of the Markov chain. (c) What proportion of time does the Markov Chain spend in state 2, in the long run? (d) Suppose X5 = 1. What is the expected additional number of steps (after time 5) until the first time the Markov chain will return to state 1