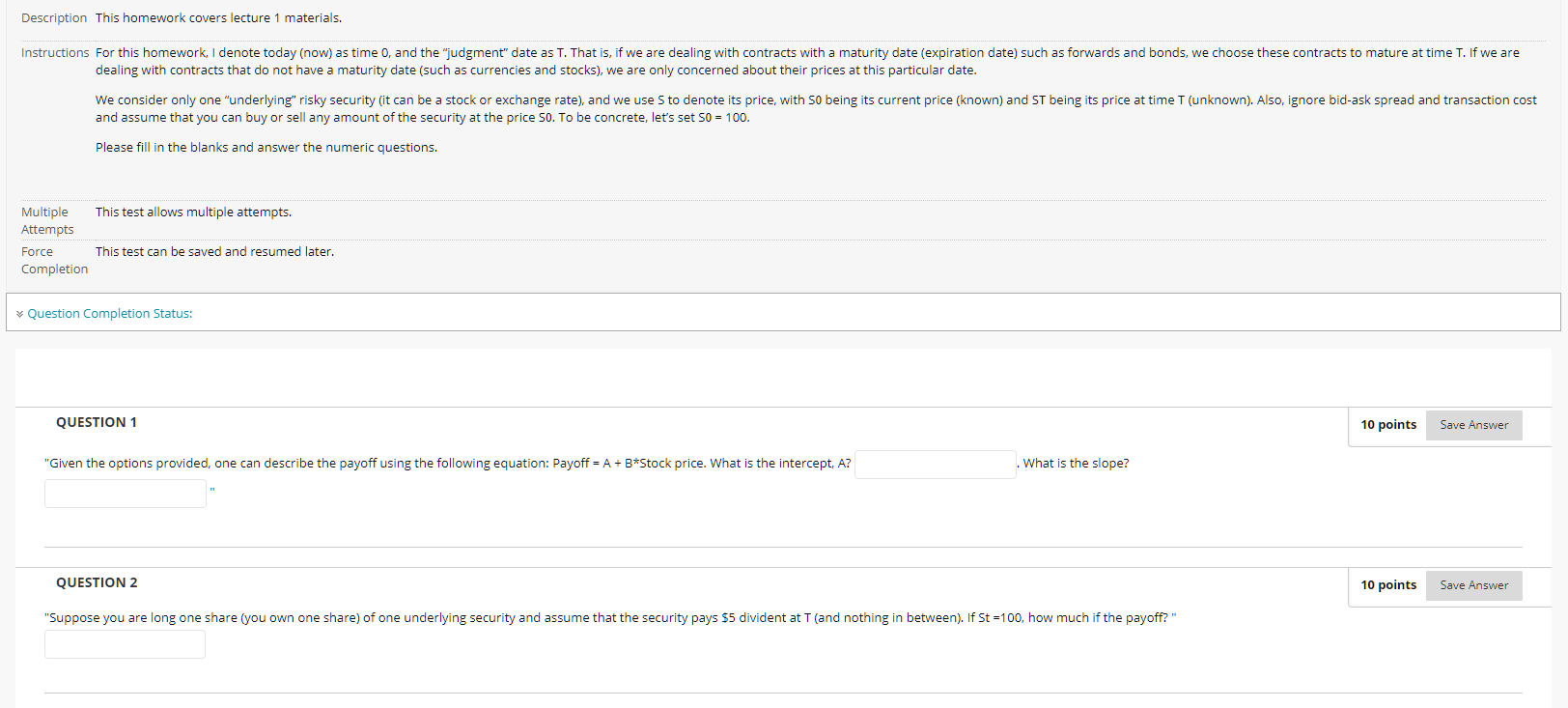
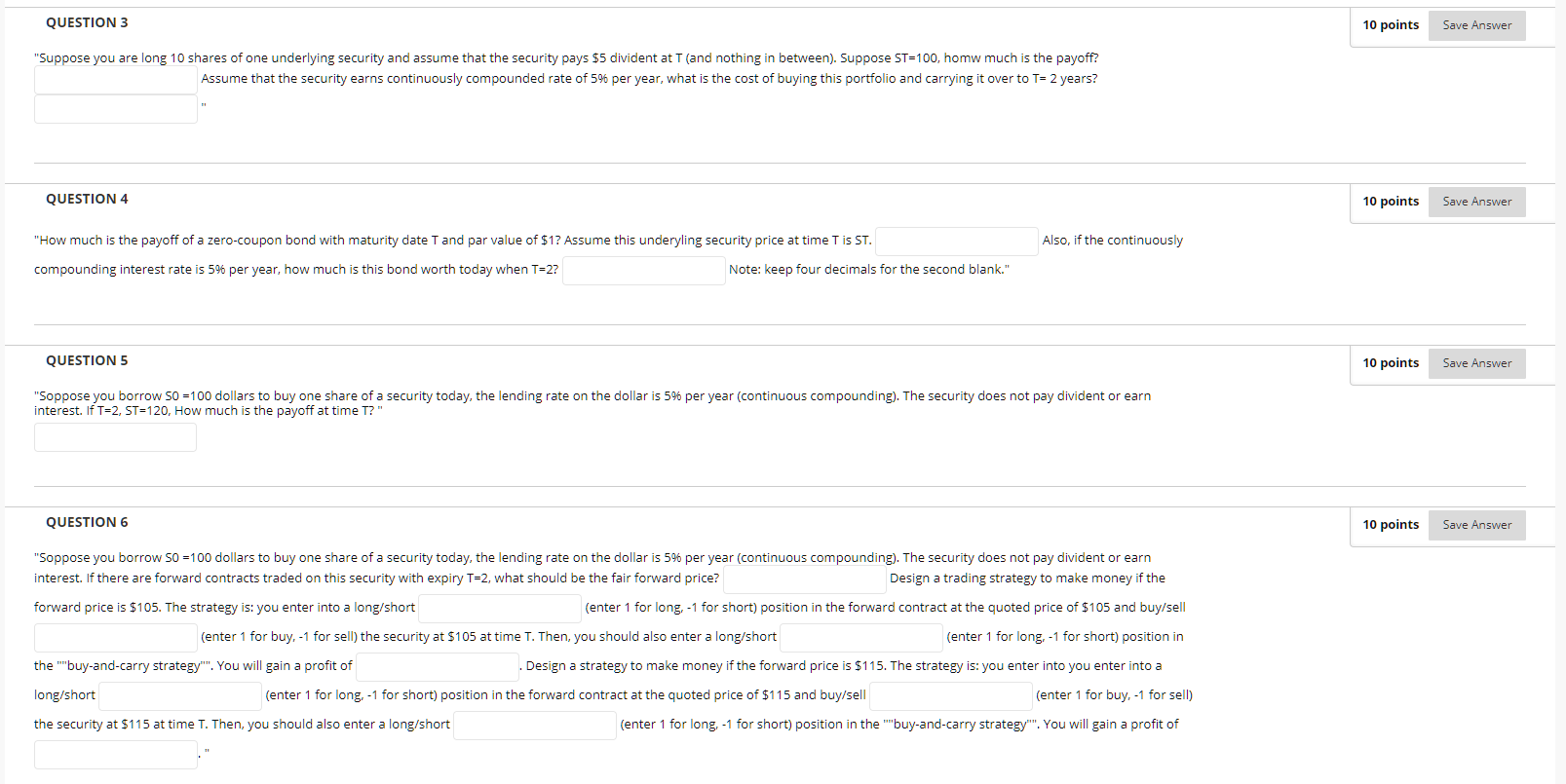
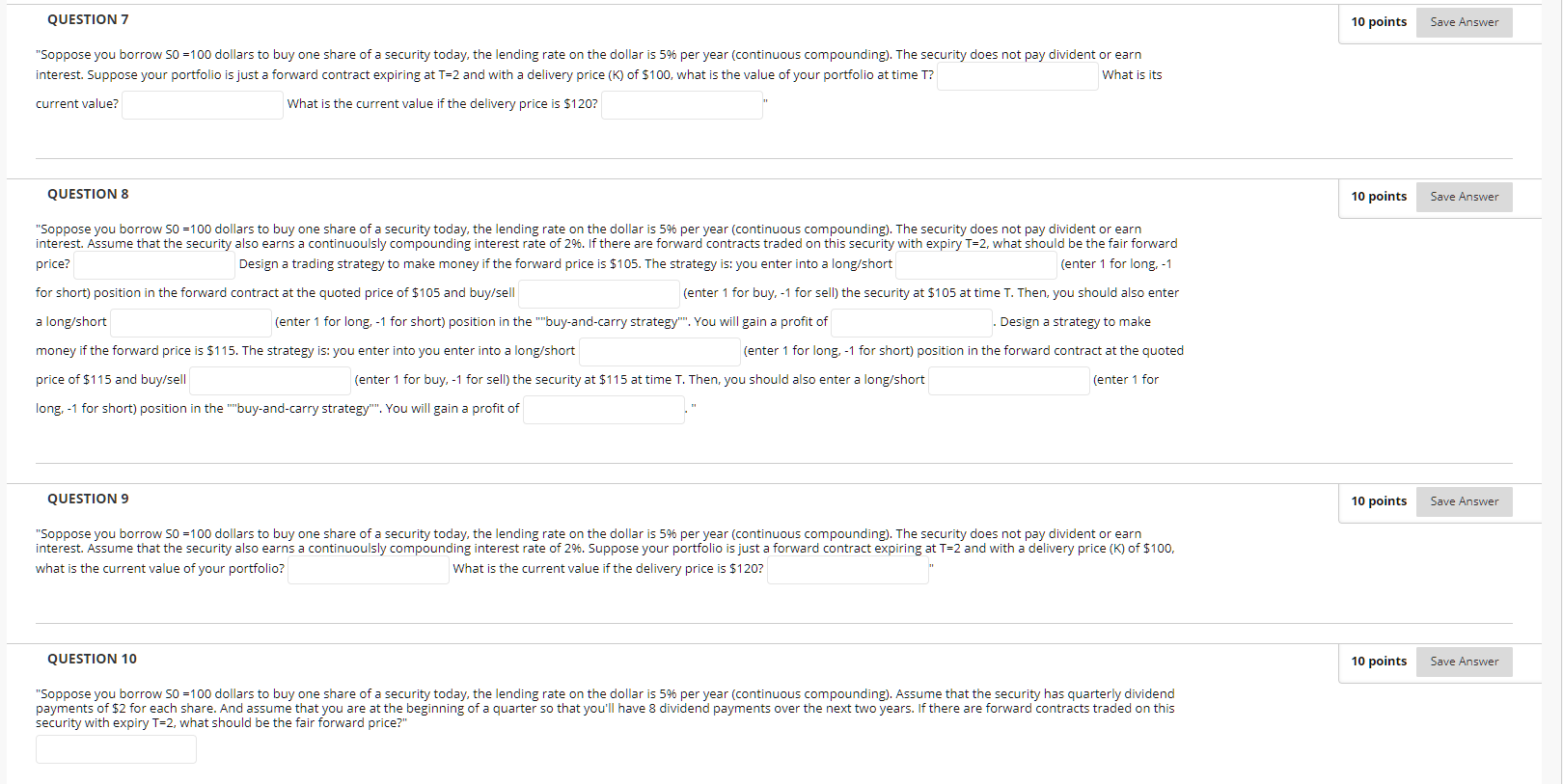
Description This homework covers lecture 1 materials. Instructions For this homework, I denote today (now) as time 0, and the "judgment" date as T. That is, if we are dealing with contracts with a maturity date (expiration date) such as forwards and bonds, we choose these contracts to mature at time T. If we are dealing with contracts that do not have a maturity date (such as currencies and stocks), we are only concerned about their prices at this particular date. We consider only one "underlying" risky security (it can be a stock or exchange rate), and we use S to denote its price, with 50 being its current price (known) and ST being its price at time T (unknown). Also, ignore bid-ask spread and transaction cost and assume that you can buy or sell any amount of the security at the price 50. To be concrete, let's set 50 = 100. Please fill in the blanks and answer the numeric questions. This test allows multiple attempts. Multiple Attempts Force Completion This test can be saved and resumed later. Question Completion Status: QUESTION 1 10 points Save Answer "Given the options provided, one can describe the payoff using the following equation: Payoff = A + B*Stock price. What is the intercept, A? . What is the slope? QUESTION 2 10 points Save Answer "Suppose you are long one share you own one share) of one underlying security and assume that the security pays $5 divident at T (and nothing in between). If St=100, how much if the payoff?" QUESTION 3 10 points Save Answer "Suppose you are long 10 shares of one underlying security and assume that the security pays $5 divident at T (and nothing in between). Suppose ST=100, homw much is the payoff? Assume that the security earns continuously compounded rate of 5% per year, what is the cost of buying this portfolio and carrying it over to T= 2 years? QUESTION 4 10 points Save Answer "How much is the payoff of a zero-coupon bond with maturity date T and par value of $1? Assume this underyling security price at time T is ST. Also, if the continuously compounding interest rate is 5% per year, how much is this bond worth today when T=2? Note: keep four decimals for the second blank." QUESTION 5 10 points Save Answer "Soppose you borrow S0 =100 dollars to buy one share of a security today, the lending rate on the dollar is 5% per year (continuous compounding). The security does not pay divident or earn interest. If T=2, ST=120, How much is the payoff at time T?" QUESTION 6 10 points Save Answer "Soppose you borrow 50 =100 dollars to buy one share of a security today, the lending rate on the dollar is 5% per year (continuous compounding). The security does not pay divident or earn interest. If there are forward contracts traded on this security with expiry T=2, what should be the fair forward price? Design a trading strategy to make money if the forward price is $105. The strategy is: you enter into a long/short (enter 1 for long-1 for short) position in the forward contract at the quoted price of $105 and buy/sell (enter 1 for buy, -1 for sell) the security at $105 at time T. Then, you should also enter a long/short (enter 1 for long, -1 for short) position in the "buy-and-carry strategy". You will gain a profit of Design a strategy to make money if the forward price is $115. The strategy is: you enter into you enter into a long/short (enter 1 for long, -1 for short) position in the forward contract at the quoted price of $115 and buy/sell (enter 1 for buy, -1 for sell) the security at $115 at time T. Then, you should also enter a long/short (enter 1 for long, -1 for short) position in the "buy-and-carry strategy""". You will gain a profit of QUESTION 7 10 points Save Answer "Soppose you borrow 50 =100 dollars to buy one share of a security today, the lending rate on the dollar is 5% per year (continuous compounding). The security does not pay divident or earn What is its interest. Suppose your portfolio is just a forward contract expiring at T-2 and with a delivery price (K) of $100, what is the value of your portfolio at time T? current value? What is the current value if the delivery price is $120? QUESTION 8 10 points Save Answer "Soppose you borrow S0 =100 dollars to buy one share of a security today, the lending rate on the dollar is 5% per year (continuous compounding). The security does not pay divident or earn interest. Assume that the security also earns a continuously compounding interest rate of 2%. If there are forward contracts traded on this security with expiry T=2, what should be the fair forward price? Design a trading strategy to make money if the forward price is $105. The strategy is: you enter into a long/short (enter 1 for long, -1 for short) position in the forward contract at the quoted price of $105 and buy/sell (enter 1 for buy, -1 for sell) the security at $105 at time T. Then, you should also enter a long/short (enter 1 for long-1 for short) position in the "buy-and-carry strategy. You will gain a profit of Design a strategy to make money if the forward price is $115. The strategy is: you enter into you enter into a long/short (enter 1 for long, -1 for short) position in the forward contract at the quoted price of $115 and buy/sell (enter 1 for buy, -1 for sell) the security at $115 at time 1. Then, you should also enter a long/short (enter 1 for long, -1 for short) position in the "buy-and-carry strategy". You will gain a profit of QUESTION 9 10 points Save Answer "Soppose you borrow 50 =100 dollars to buy one share of a security today, the lending rate on the dollar is 5% per year (continuous compounding). The security does not pay divident or earn interest. Assume that the security also earns a continuoulsly compounding interest rate of 296. Suppose your portfolio is just a forward contract expiring at T=2 and with a delivery price (K) of $100, what is the current value of your portfolio? What is the current value if the delivery price is $120? QUESTION 10 10 points Save Answer "Soppose you borrow 50 =100 dollars to buy one share of a security today, the lending rate on the dollar is 596 per year (continuous compounding). Assume that the security has quarterly dividend payments of $2 for each share. And assume that you are at the beginning of a quarter so that you'll have 8 dividend payments over the next two years. If there are forward contracts traded on this security with expiry T-2, what should be the fair forward price