Design decrease-by-half algorithm that solves the problem; describe your algorithm with clear pseudocode; and prove the time efficiency class of your algorithm

def perfectBST(V):

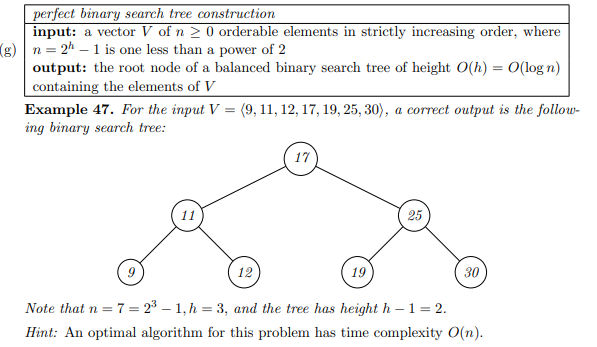
perfect binary search tree construction input: a vector V of n > 0 orderable elements in strictly increasing order, where (g) n = 2h - 1 is one less than a power of 2 output: the root node of a balanced binary search tree of height O(h) = O(log n) containing the elements of V Example 47. For the input V = (9, 11, 12, 17, 19, 25, 30), a correct output is the follow- ing binary search tree: 17 11 25 12 19 30 Note that n= 7 = 23 1, h = 3, and the tree has height h-1= 2. Hint: An optimal algorithm for this problem has time complexity O(n)