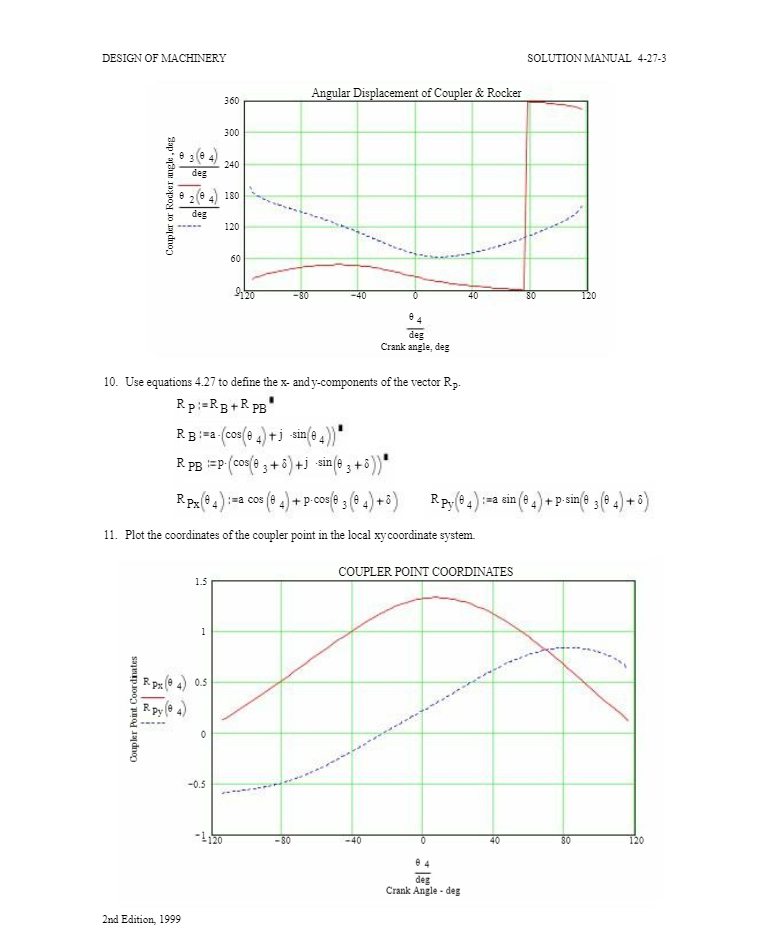
DESIGN OF MACHINERY SOLUTION MANUAL 4-27-1 PROBLEM 4-27 Statement: For the linkage in Figure P4-13, find its limit (toggle) positions in terms of the angle of link O4B referenced to the line of centers 040, when driven from link OB. Then calculate and plot the angular displacement of links 2 and 3 and the path coordinates of point P with respect to the angle of the input crank O&B over its possible range of motion referenced to the line of centers 040. Given: Link lengths: Input (O+B) a=0.86 Coupler (AB) b=1.85 Rocker (OA) C=0.86 Ground link d:= 2.22 Coupler point data: p=0.52 8 = 0.deg Two argument inverse tangent atan2(x,y) = retum 0.5. if x=0 retum atan if x>0 atan + otherwise 116.037 b B y Solution: See Figure P4-13 and Mathcad file P0427. 1. Check the Grashof condition of the linkage. Condition(S,L, P, Q) = |SL+S+L PQ-P+Q return "Grashof" if SL SPQ return "non-Grashof" otherwise Condition(a, d, b, c) = "non-Grashof" 2. Using equations 4.33, determine the crank angles (relative to the line 040) at which links 2 and 3 are in toggle. 2 (a)+(d)-(b)-(c) b.c arg 1 == (2a d) (a.d) arg 1 = 1.228 (a)+(d) - (b) - (c) arg 2 (2 a d) b.c (a.d) arg 2 = -0.439 acos (arg 2) 4toggle = 116.037 deg 8 4toggle The other toggle angle is the negative of this. 3. Define one cycle of the input crank between limit positions: 4 2nd Edition, 1999 4toggle-toggle +2. deg. 4toggle DESIGN OF MACHINERY 4. Use equations 4.8a and 4.10 to calculate 02 as a function of 04 (for the open circuit). d d SOLUTION MANUAL 4-27-2 a-b+c+d K = a K1=2.5814 K2" K2=2.5814 A(04) = cos(4)-K1-K2-cos (4)+K3 B(04)=-2-sin(84) K3 (2-ac) K3=2.0181 C(84) = 1 - (K2+1) cos(84)+K 3 8 21(84)=2(atan2 (2.4(84).-B(84) - B(84) - 4A(84)C(84))) 5. If the calculated value of 0, is greater than 2, subtract 2 from it. If it is negative, make it positive. 22(4) 21 (4)>2,8 21 (4)-2-, 21 (04)) 02 (4) 22 (4) 2-, 31 (4)-2, 31 (04)) == 83(04) 32 (4)