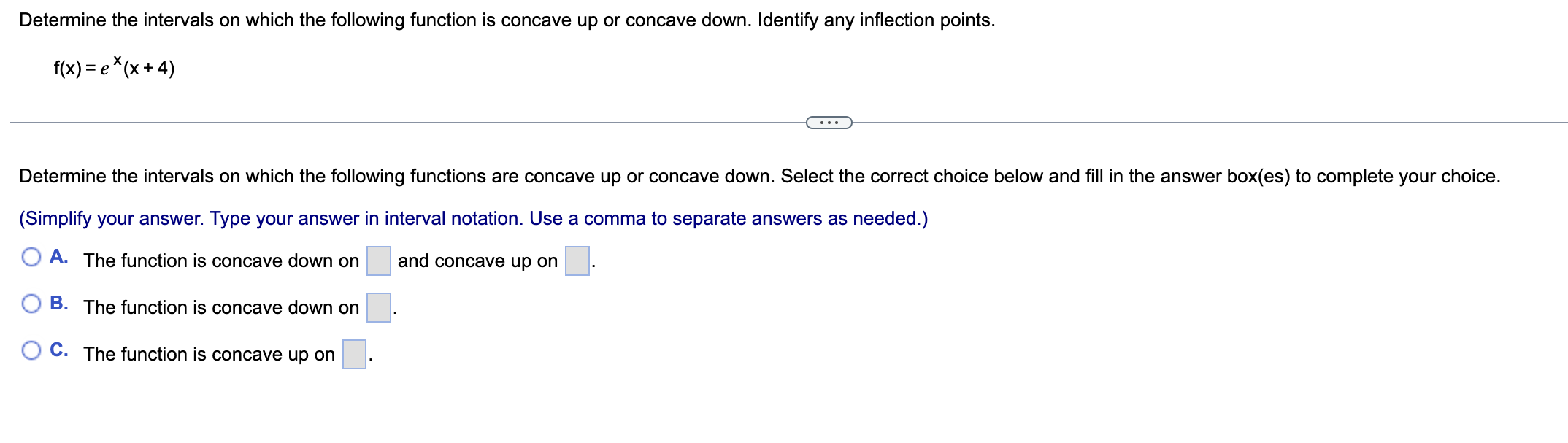
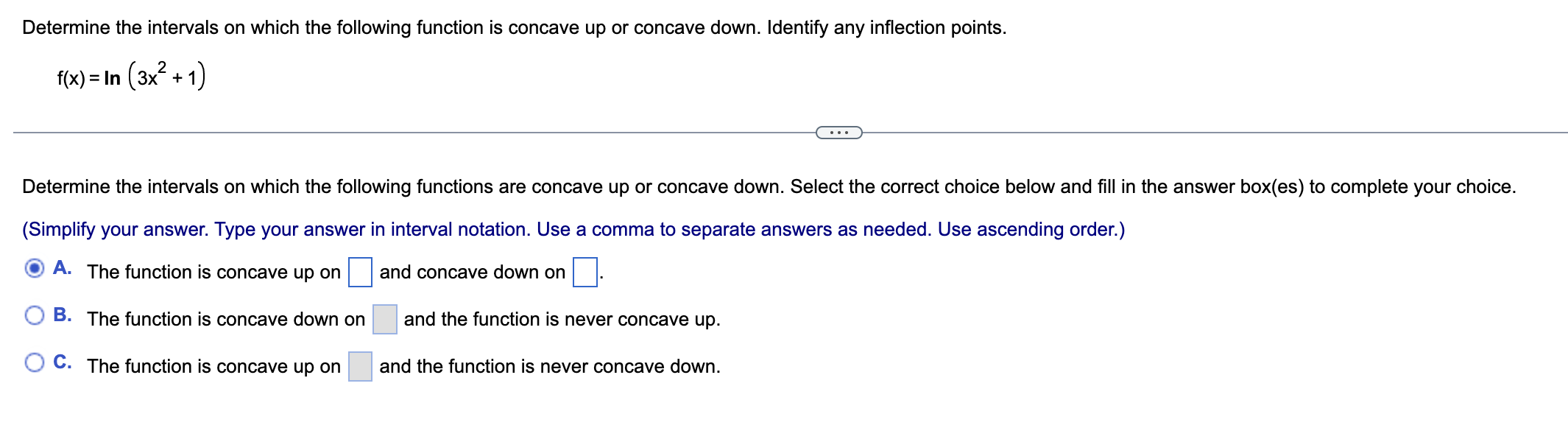
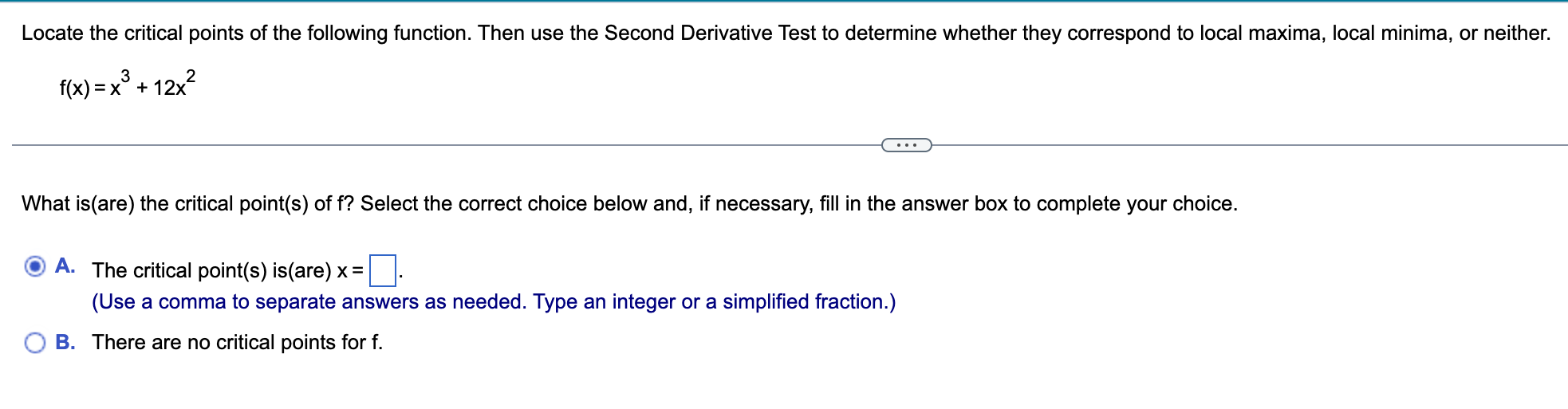
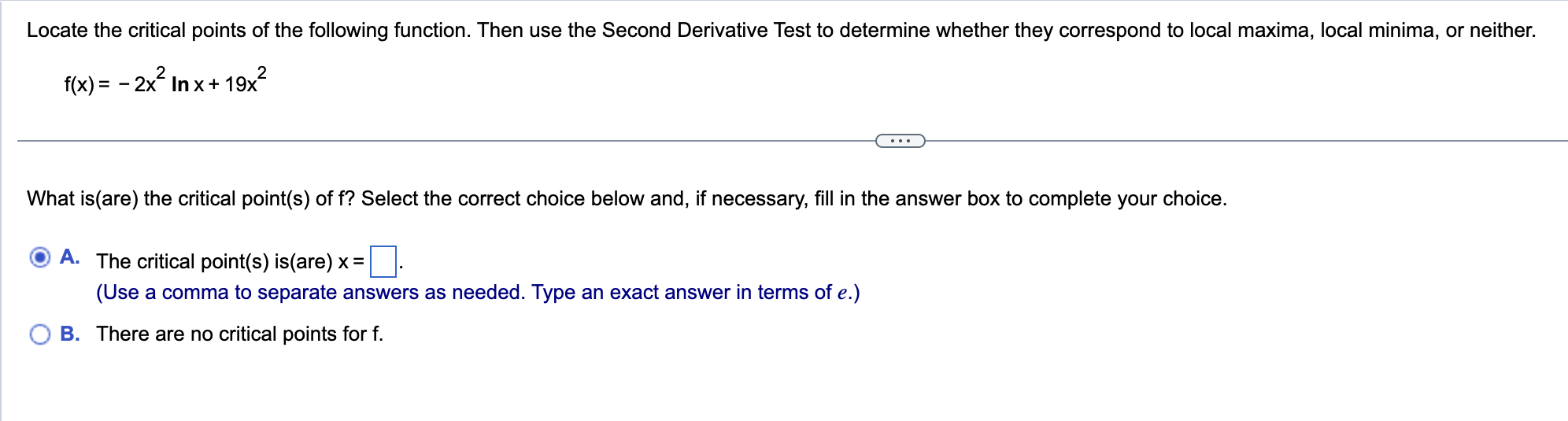
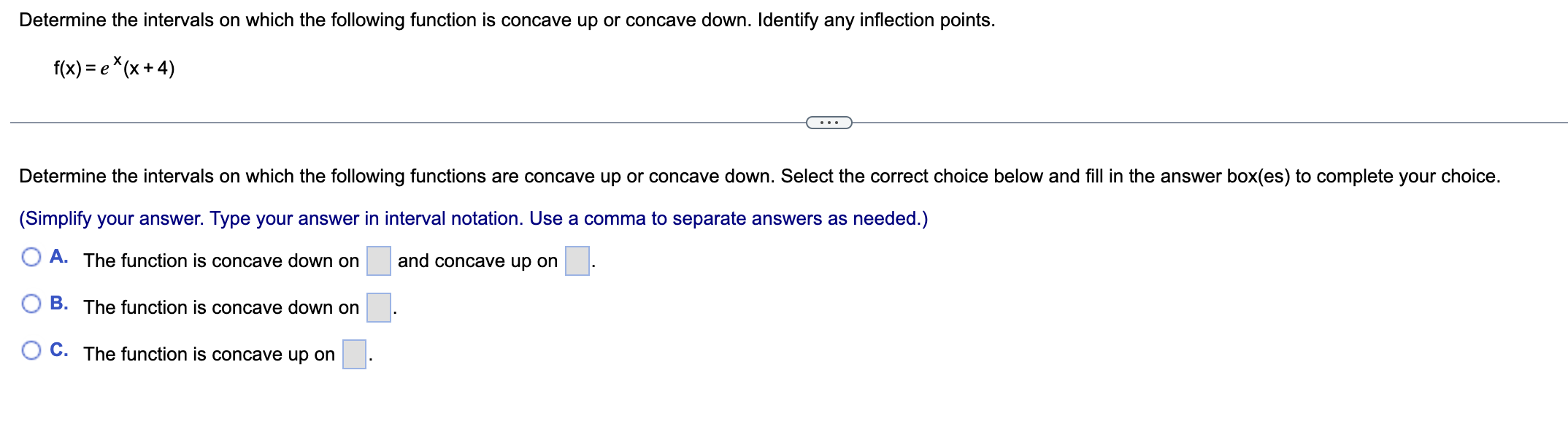
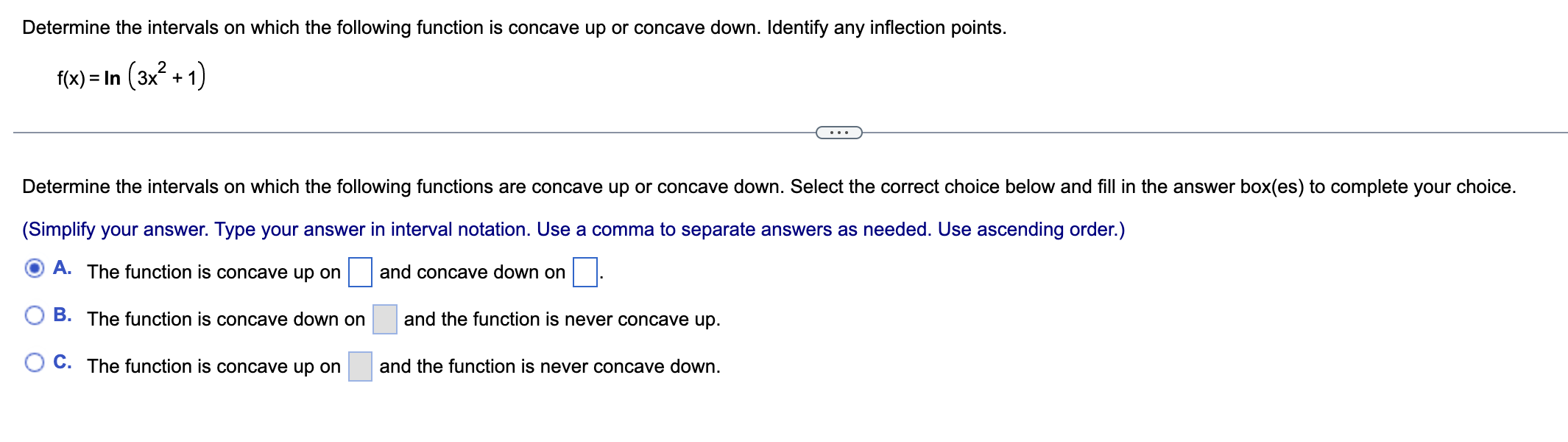
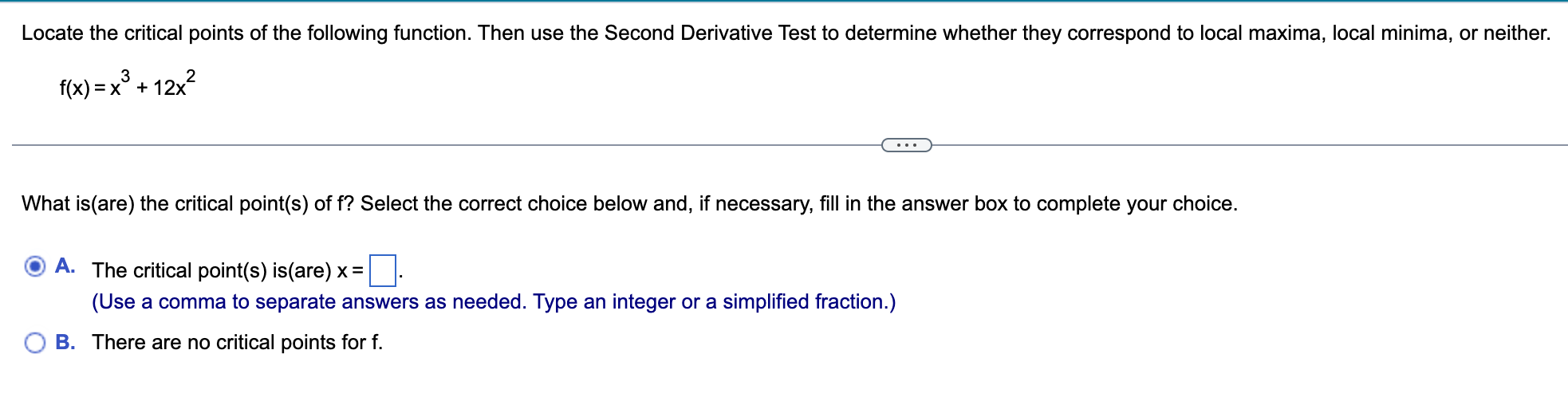
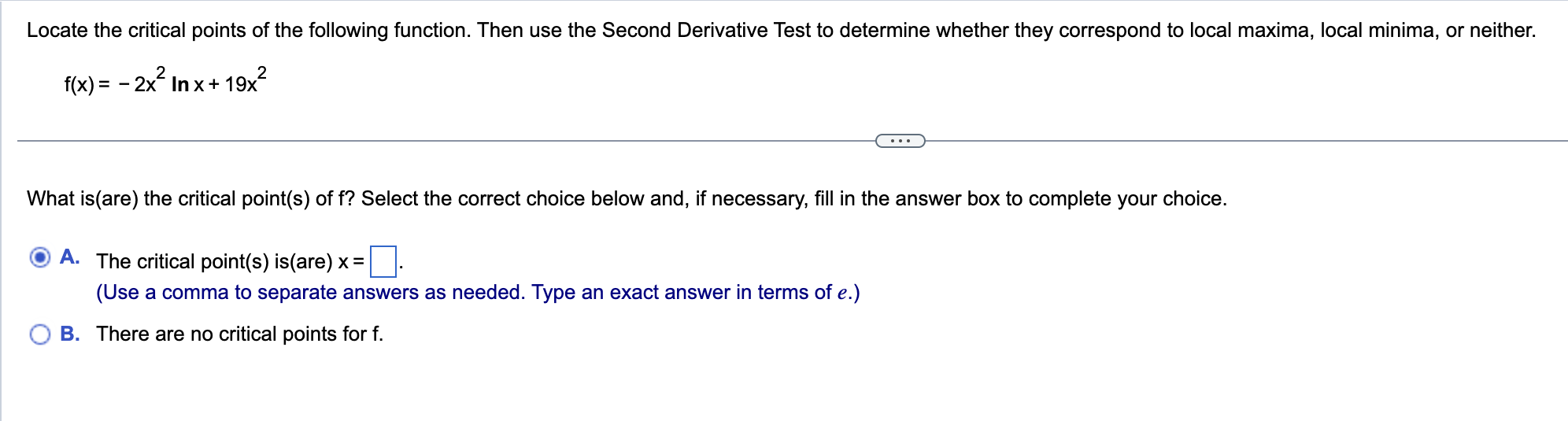
Determine the intervals on which the following function is concave up or concave down. Identify any inflection points. f(x) = e (x+4) . . . Determine the intervals on which the following functions are concave up or concave down. Select the correct choice below and fill in the answer box(es) to complete your choice. (Simplify your answer. Type your answer in interval notation. Use a comma to separate answers as needed.) O A. The function is concave down on and concave up on O B. The function is concave down on O C. The function is concave up onDetermine the intervals on which the following function is concave up or concave down. Identify any inflection points. f(x)=ln (3x2 +1) Determine the intervals on which the following functions are concave up or concave down. Select the correct choice below and ll in the answer box(es) to complete your choice. (Simplify your answer. Type your answer in interval notation. Use a comma to separate answers as needed. Use ascending order.) A- The function is concave up on :| and concave down on '33.} B- The function is concave down on and the function is never concave up. '33.:3' C. The function is concave up on and the function is never concave down. Locate the critical points of the following function. Then use the Second Derivative Test to determine whether they correspond to local maxima. local minima. or neither. f(x) = x3 +12x2 E) What is(are) the critical point(s) of f? Select the correct choice below and, if necessary, fill in the answer box to complete your choice. {'3 A- The critical point(s) is(are) x= El. (Use a comma to separate answers as needed. Type an integer or a simplified fraction.) {:3 B. There are no critical points for f. Locate the critical points of the following function. Then use the Second Derivative Test to determine whether they correspond to local maxima, local minima, or neither. f(x)= - 2x2|nx+19x2 What is(are) the critical point(s) of f? Select the correct choice below and, if necessary, fill in the answer box to complete your choice. '33\" A- The critical point(s) is(are) X: D. (Use a comma to separate answers as needed. Type an exact answer in terms of e.) {:23 B. There are no critical points for f