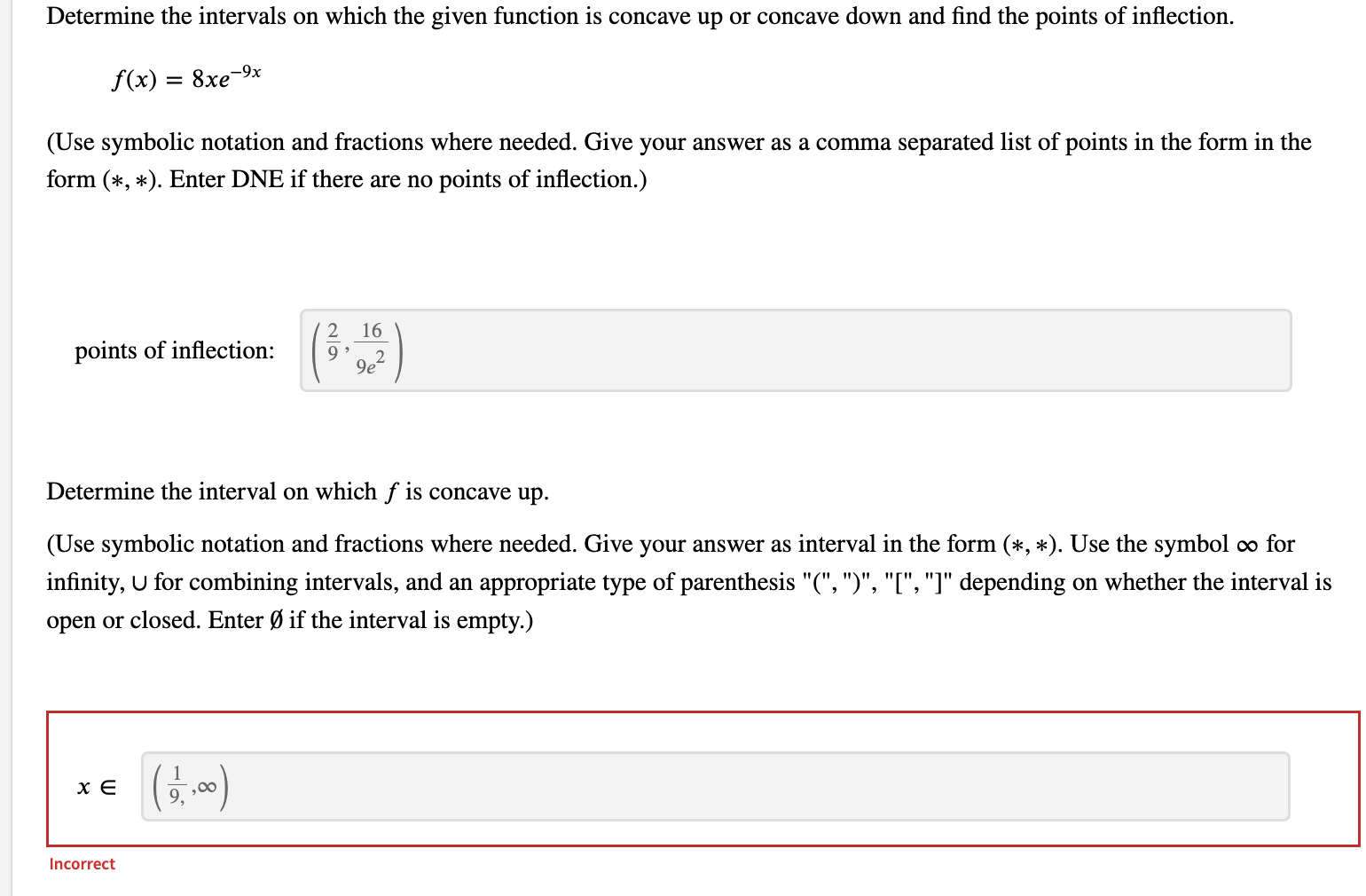
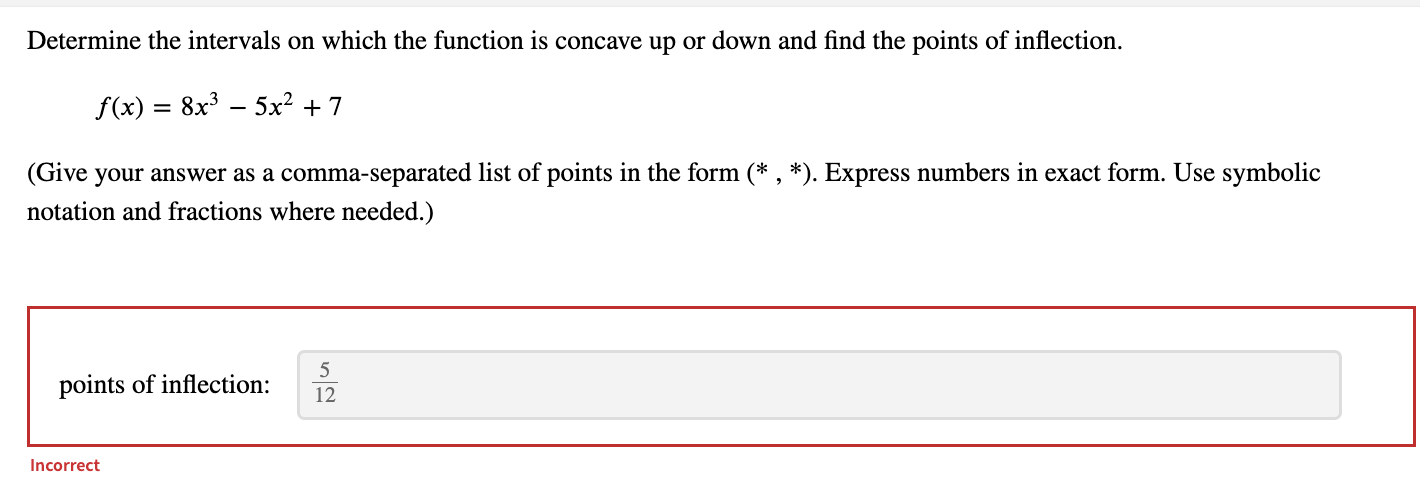
Question: Determine the intervals on which the given function is concave up or concave down and find the points of inflection. f(x) = 8xe-9x (Use symbolic


![")", "[", "]" depending on whether the interval is open or closed.](https://s3.amazonaws.com/si.experts.images/answers/2024/06/6664d4dd2369c_1256664d4dd0d49a.jpg)
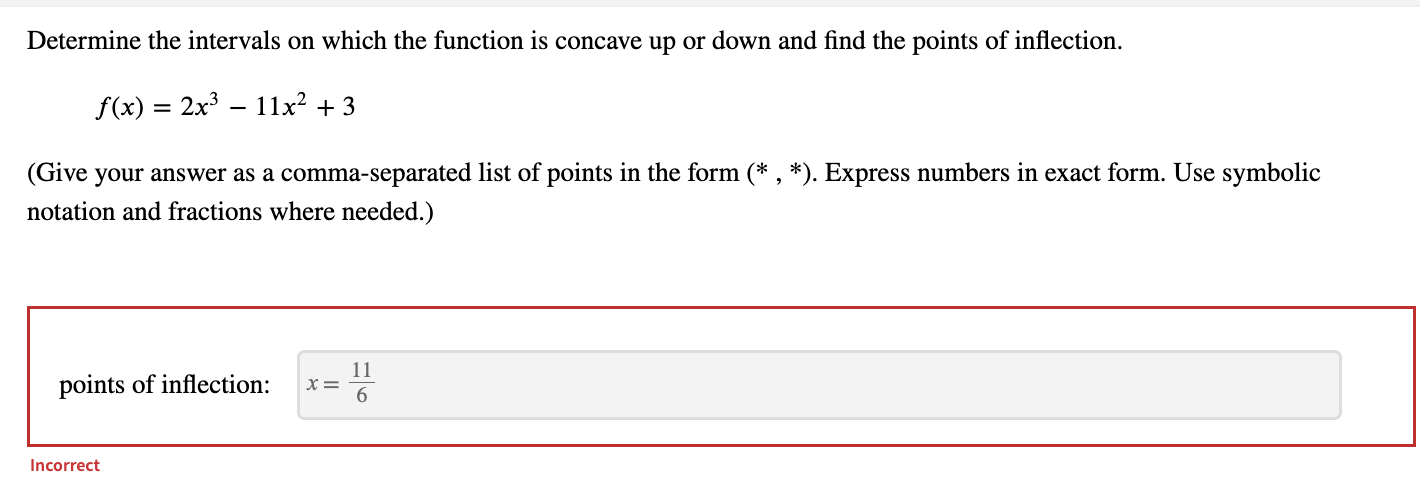
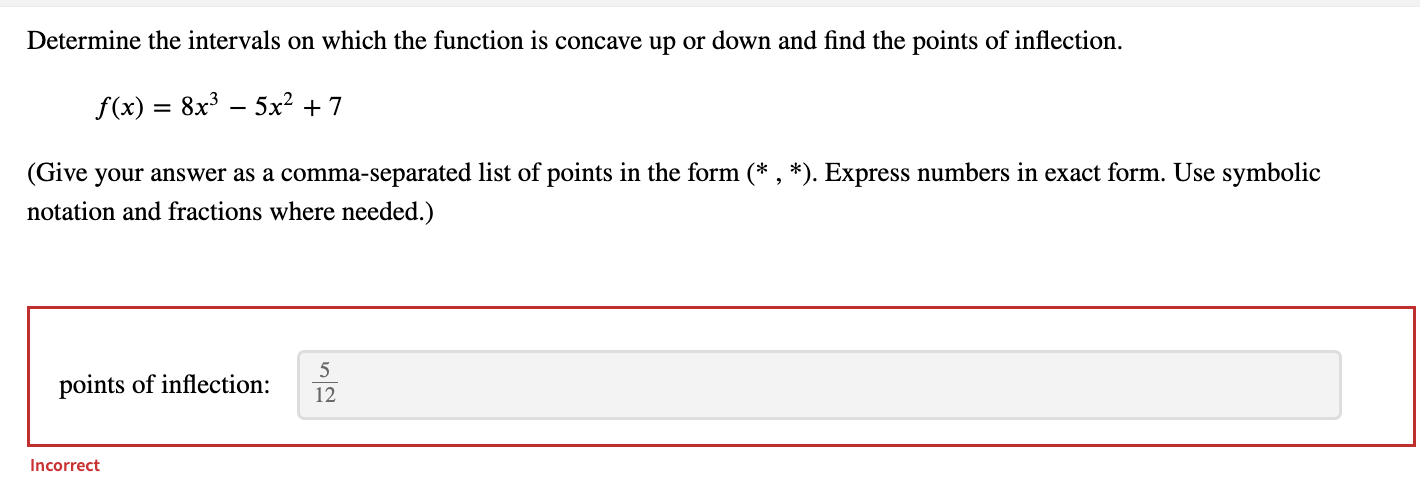
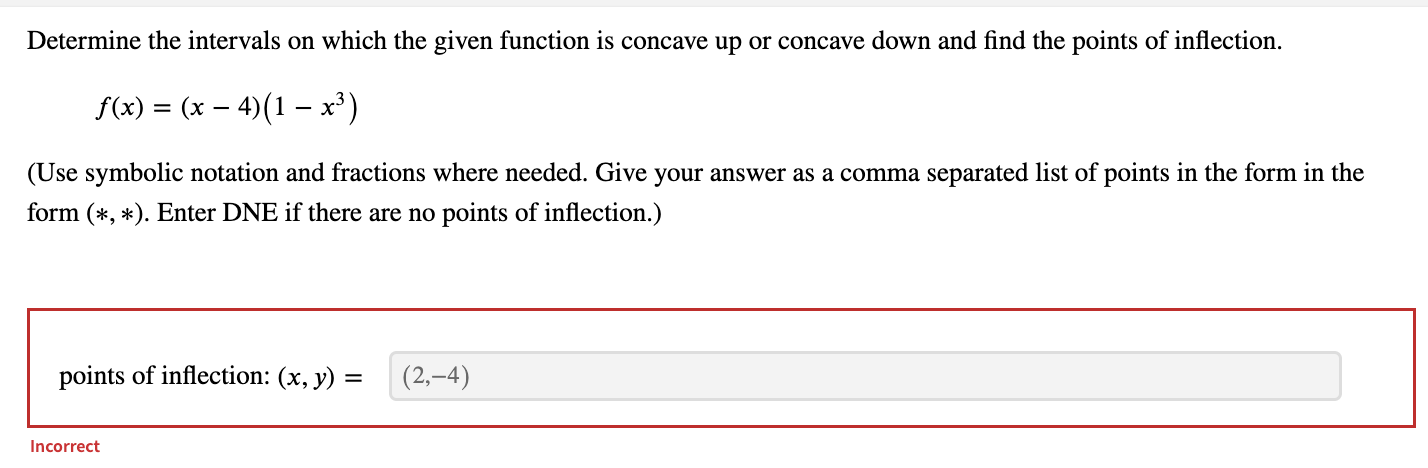
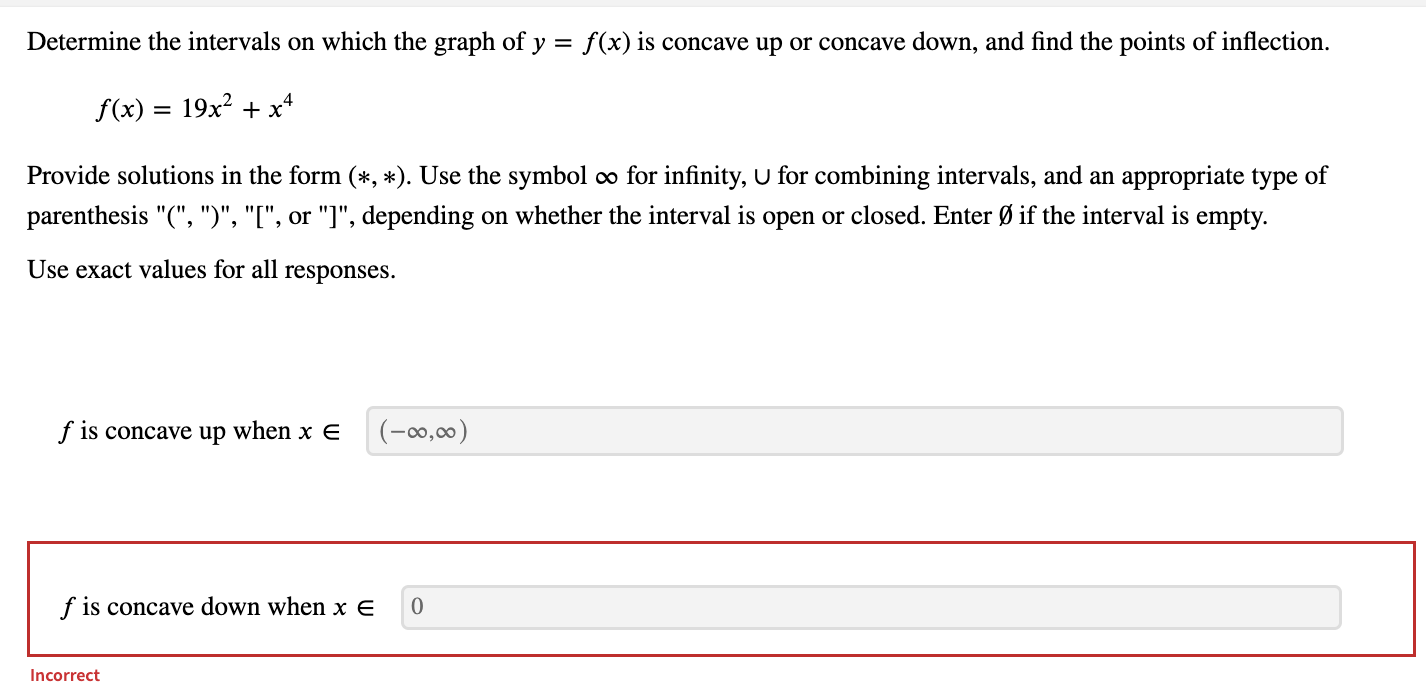
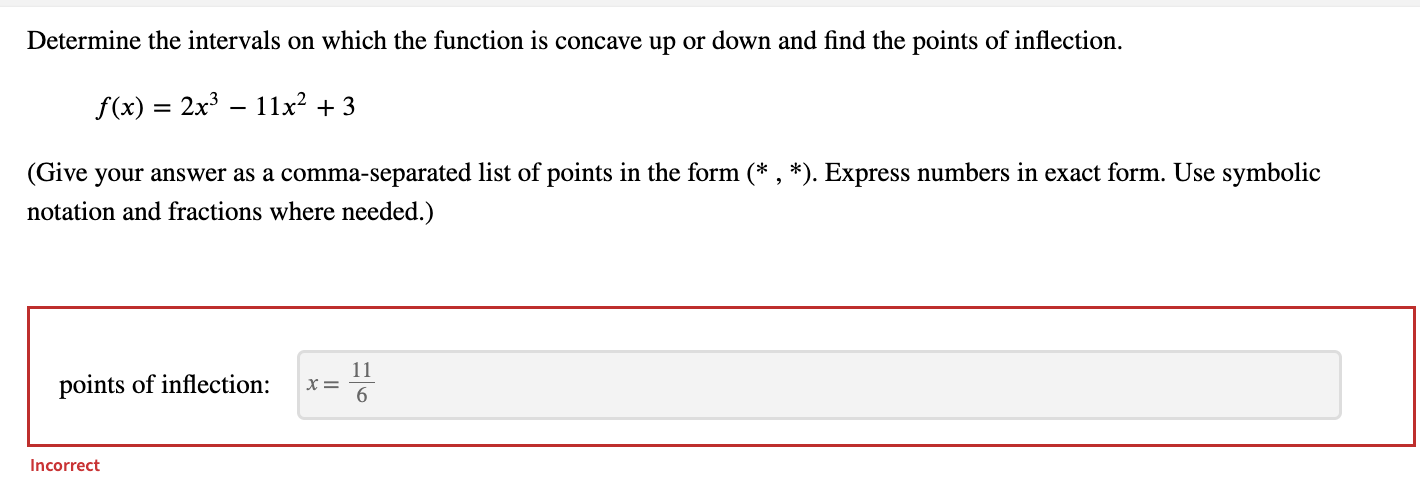
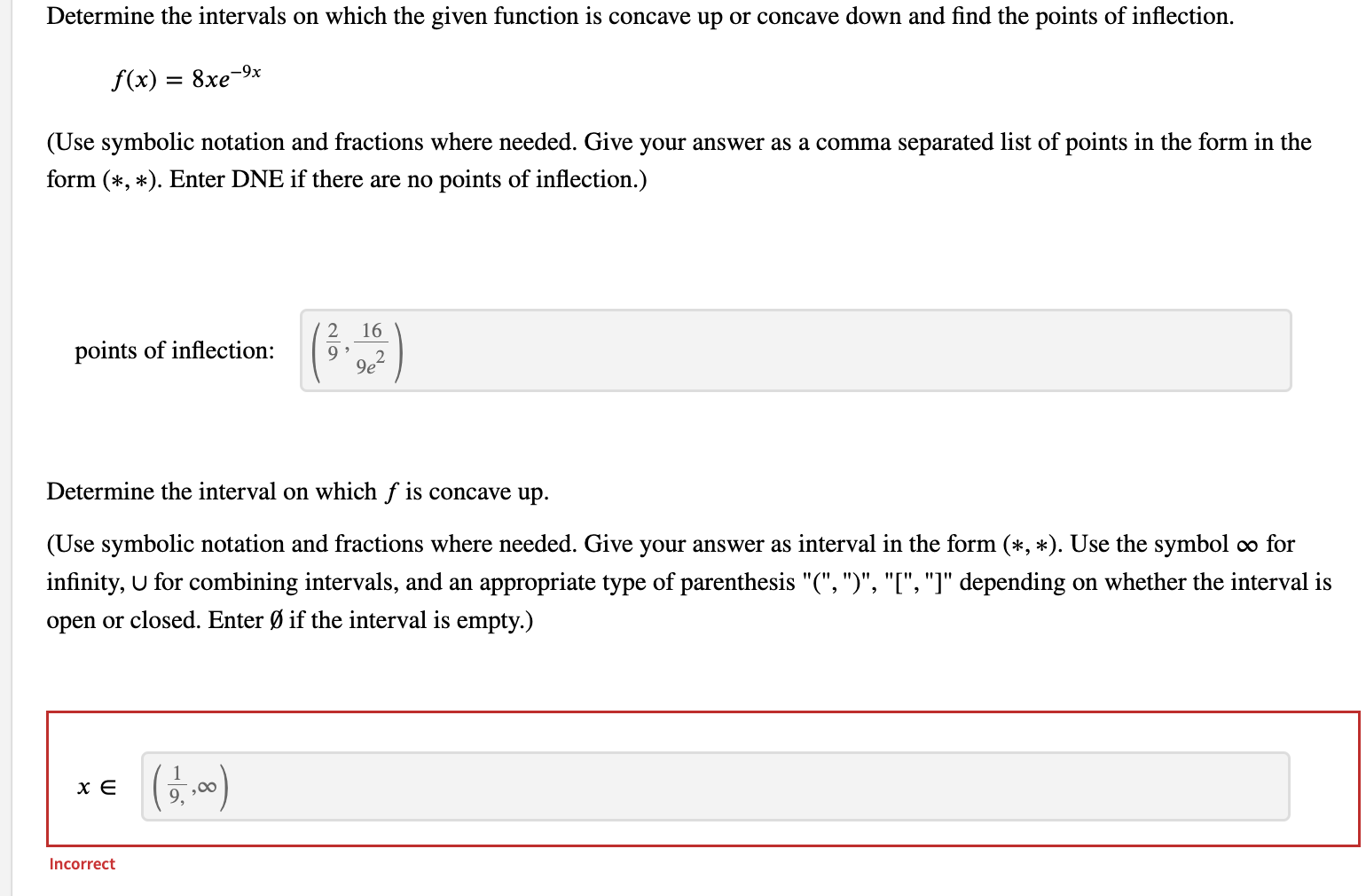
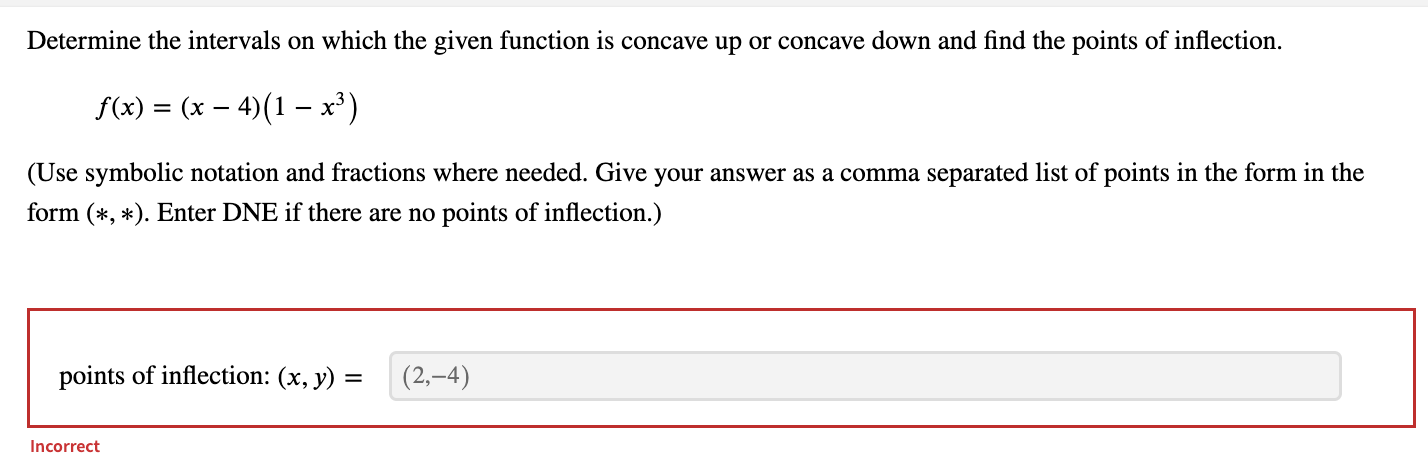
Determine the intervals on which the given function is concave up or concave down and find the points of inflection. f(x) = 8xe-9x (Use symbolic notation and fractions where needed. Give your answer as a comma separated list of points in the form in the form (*, *). Enter DNE if there are no points of inflection.) 2 16 points of inflection: 9 ge2 Determine the interval on which f is concave up. (Use symbolic notation and fractions where needed. Give your answer as interval in the form (*, *). Use the symbol co for infinity, U for combining intervals, and an appropriate type of parenthesis "(", ")", "[", "]" depending on whether the interval is open or closed. Enter ( if the interval is empty.) X E 9 .,00 IncorrectDetermine the intervals on which the function is concave up or down. w(t) = + 2 (Give your answer as an interval in the form (*, *). Use the symbol co for infinity, U for combining intervals, and an appropriate type of parenthesis "(",")", "[","]" depending on whether the interval is open or closed. Enter O if the interval is empty. Express numbers in exact form. Use symbolic notation and fractions where needed.) w is concave up on w is concave down on - 0o , - 3 ) U (0 . 13 7 ) Find the point(s) of inflection. Give your answer as a comma-separated list of points in the form (*, *). Express numbers in exact form. Use symbolic notation and fractions where needed. Enter DNE if the function has no inflection points.) 29/3 inflection point(s): 1/27 3 3 + 2Determine the intervals on which the given function is concave up or concave down and find the points of inflection. f(x) = (x -4)(1 -x3) (Use symbolic notation and fractions where needed. Give your answer as a comma separated list of points in the form in the form (*, *). Enter DNE if there are no points of inflection.) points of inflection: (x, y) = (2, -4) IncorrectDetermine the intervals on which the graph of y = f(x) is concave up or concave down, and find the points of inflection. f(x) = 19x2 + x4 Provide solutions in the form (*, *). Use the symbol co for infinity, U for combining intervals, and an appropriate type of parenthesis "(", ")", "[", or "]", depending on whether the interval is open or closed. Enter O if the interval is empty. Use exact values for all responses. f is concave up when x E (-00,00) f is concave down when x E 0 IncorreDetermine the intervals on which the function is concave up or down and find the points of inflection. f(x) =2x3 - 11x2 + 3 (Give your answer as a comma-separated list of points in the form (* , *). Express numbers in exact form. Use symbolic notation and fractions where needed.) points of inflection: 11 X = 6 IncorrectDetermine the intervals on which the function is concave up or down and find the points of inflection. f(x) = 8x3 - 5x2+7 (Give your answer as a comma-separated list of points in the form (* , *). Express numbers in exact form. Use symbolic notation and fractions where needed.) points of inflection: 5 12 Incorrect
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


