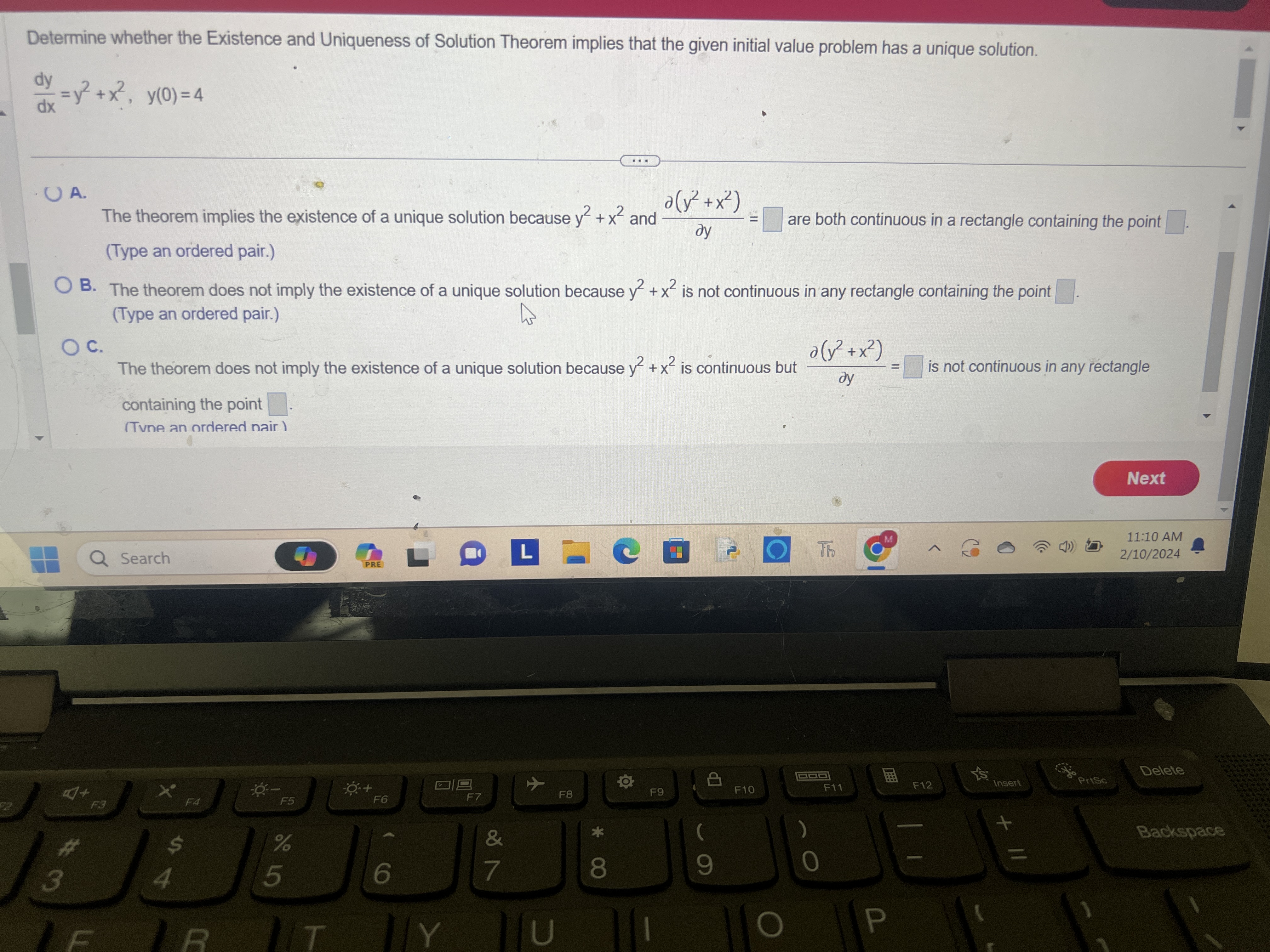
Determine whether the Existence and Uniqueness of Solution Theorem implies that the given initial value problem has a unique solution. Y242, y(0)=4 =y 4 - dx y +x, y0) O A : i . 9 2 d(yz it Xz) 5 The theorem implies the existence of a unique solution because y* +x\" and - ;)y =| | are both continuous in a rectangle containing the point o (Type an ordered pair.) f O B. The theorem does not imply the existence of a unique solution because y7 +X\" is not continuous in any rectangle containing the point " ,' (Type an ordered pair.) [\\\\; i 9 15 a(y' +x) _ | 2 s continuous but T =/ |is not continuous in any rectangle i 8 3 C. The theorem does not imply the existence of a unique solution because y2 +X containing the point (Tvne an ardered nair \\ N O DD 000 B 4 %= Q Search