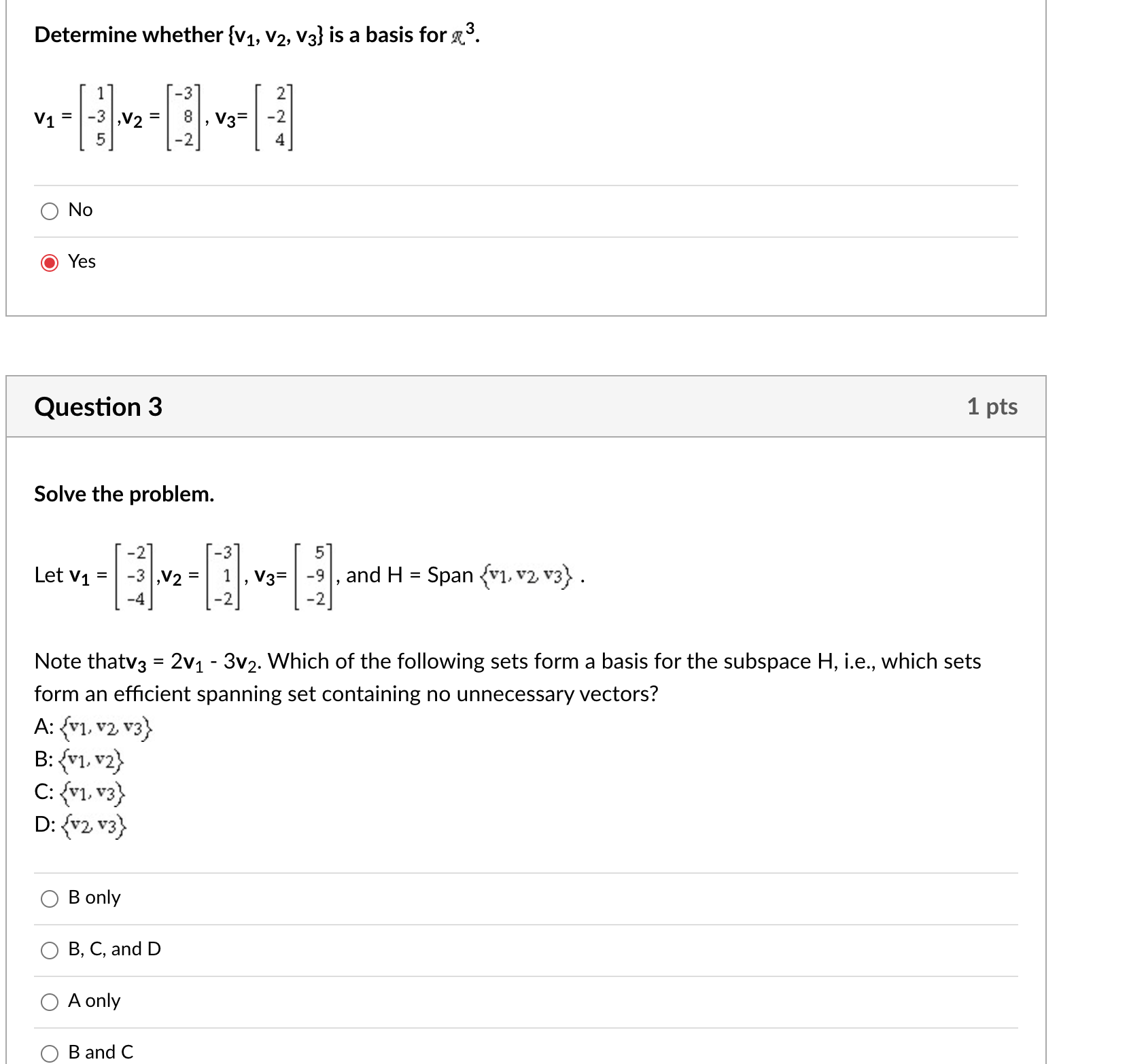
Question: Determine whether {V1, V2, V3) is a basis for a 3. V1 -3 , V2 = 8 N N O No Yes Question 3 1

Determine whether {V1, V2, V3) is a basis for a 3. V1 -3 , V2 = 8 N N O No Yes Question 3 1 pts Solve the problem. Let v1 = -3 ,v2= ; , v3- -3 , and H = span { v1 , v2 3 } . Note thatv3 = 2v1 - 3v2. Which of the following sets form a basis for the subspace H, i.e., which sets form an efficient spanning set containing no unnecessary vectors? A: {v1, v2 V3} B: {V1, v2} C: {V1, V3} D: {V2 V3} O B only O B, C, and D O A only O B and C

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

n Yes Question 4 Solve the problem. Let V = -3,V2 = Note thatv3 = 2v - 3v2. Which of the following sets form a basis for the subspace H, i.e., which sets form an efficient spanning set containing no...

ignore the lines and solve each question separately please Q Let B (V1, V2, V3, V4] be a basis for R4. Let TRR be the linear transformation such that on the basis vectors V1, V2, V3, V4, its values...

lg ACTIVITIES Activity 1: Solve Me! Directions: Sketch the diagram for each item and solve what is being asked. 1. Three capacitors with individual capacitances of 2 pF, 5 pF, and II] pF respectively...

question below: x Let H = : 8x2 + 4y2 $1 , which represents the set of points on and inside an ellipse in the xy-plane. Find two Y specic examplestwo vectors, and a vector and a scalarto show that H...

Suppose a bond with annual coupons has a price of $1,071.06, a face value of $1000 and a yield to maturity of 7%. This bond's coupon rate is closest to: PS. There is no missing data in this question....

In details only, please! Thanks! A: Diseases B: Symptom P(A) a a1 P(BIA) P(BA) b 0.2 bi 0.3 0.7 ao 0.8 B a1 0.4 0.6 Figure 3: Probabilistic Graph of Diseases and Sympton 7. Use the information...

To see that composition of two rotations about different coordination axes is equivalent to a single rotation about a fixed direction. M=[1 2 3; 4 5 6] Creates a certain 2 times 3 matrix and calls it...

Consider the following set of vectors. 3 V = V 4 Let V, V2, and V3 be (column) vectors in R3 and let A be the 3 x 3 matrix [V1 V2 V3] with these vectors as its columns. Then V, V2, and v3 are...

Please finish this program. In this assignment, you will build a system that simulates a simple network. In this network, it is possible to send a text message between any two nodes (vertices in...

Helena Morales wants to backtest a WTI hedge versus a Brent hedge. She takes a monthly hedge position of 20 million gallons for 2012. This corresponds to a hedge totalling 240 million gallons, which...

A 30-unit apartment building should last 35 years, when it will need to be either replaced or undergo major renovation. Assume the building's value at 35 years will be 10% of its construction cost....

Last year, ABC Insurance Company had a combined ratio of 102.5 and a return on its investments (income and capital gains relative to dollars invested) of positive 2%, while XYZ Insurance Company had...

Assignment: ST 260- Assignment 7- Sampling Distributions Questions Exercise 07.19 (Sampling Distribution of x) 2 0 Save Assignment Score: 22.22% Submit Assignment for Grading Question 5 of 9 Check My...