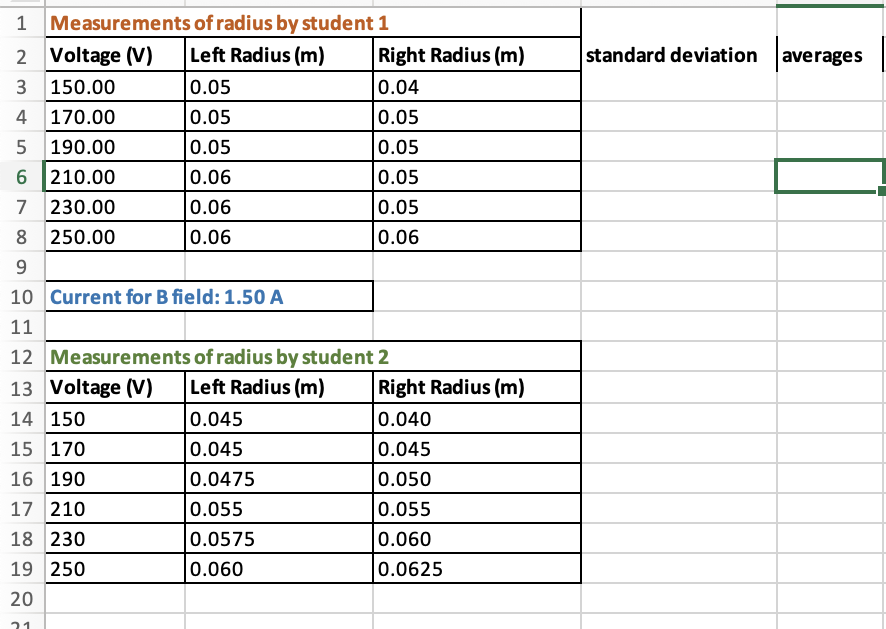
Determining the Magnetic eld The magnetic eld in this experiment is created by current in two circular coils that have parallel planes separated by one radius. This arrangement is called a set of Helmholtz coils. The apparatus front panel provides a formula for B, in which the appropriate values have been inserted: B = 7.80 x10'41 Here B is in units of Telsa and the current I is in units of Amps. Procedure and Analysis 1. The radius of the electron beam was measured and the data have been provided. 2. Use the equation provided above to determine the magnetic eld. 3. Use equation 3 to nd e/m for each case. 4. Determine the standard deviation for your data. Discuss the precision of your experiment. Are the individual measurements with associated uncertainty accurate when compared to the accepted value? 5. Find the average value and standard deviation of your measurements of e/m. Compare the average with the accepted value of 1.76x1011C/kg. Was your average value accurate? 1 Measurements of radius by student 1 2 Voltage (V) Left Radius (m) Right Radius (m) standard deviation averages 3 150.00 0.05 0.04 4 170.00 0.05 0.05 5 190.00 0.05 0.05 6 210.00 0.06 0.05 7 230.00 0.06 0.05 8 250.00 0.06 0.06 9 10 Current for B field: 1.50 A 11 12 Measurements of radius by student 2 13 Voltage (V) Left Radius (m) Right Radius (m) 14 150 0.045 0.040 15 170 0.045 0.045 16 190 0.0475 0.050 17 210 0.055 0.055 18 230 0.0575 0.060 19 250 0.060 0.0625 20In this experiment we will measure a fundamental property of the electron, the ratio of its . . (3 charge to Its mass wr1tten as '". me In the experiment, a beam of electrons accelerated by a potential difference (+V) is bent into a circular path by a magnetic eld. The beam is in a glass container containing a small amount of helium gas. Some of the electrons in the beam collide with these molecules, and this results in the emission of light. This process produces a visible track corresponding to the electron beam, so the diameter of the resulting circle of electrons may be measured by eye. Calculating the radius from the diameter, and making measurements of the +V (accelerating voltage) and the magnetic eld (B) produced by the large large coils around the electron tube the electron's charge to mass ratio is determined. The magnetic force acting perpendicular to the charged particles velocity can be written as: F=qu (l) in which q is the electric charge, v is the velocity, and B is the magnetic eld. If the magnetic field is constant, and since the velocity is acting perpendicular to the magnetic eld, the magnetic force will move the electrons into a circular path. We know from Newton's Laws and circular motion that 172 a. = and F = ma R Therefore, by substitution we can write Equation (1) as: 2 F=ma=me 1%]:(18123 (2) There is no way to determine the velocity of the electron stream directly, but the potential energy imparted to the electrons by the accelerating voltage +V can be written as: PE (from potential) = qe(+V) = KEe = garnet?2 If we solve for the velocity in the force equation (2) we nd: R v: 3* Qe me Substituting for the velocity in the energy equation we nd: R qe(+V) = me(QeB *;)2 Simplifying this equation we nd: q_, - 2V (3) me _ 3sz