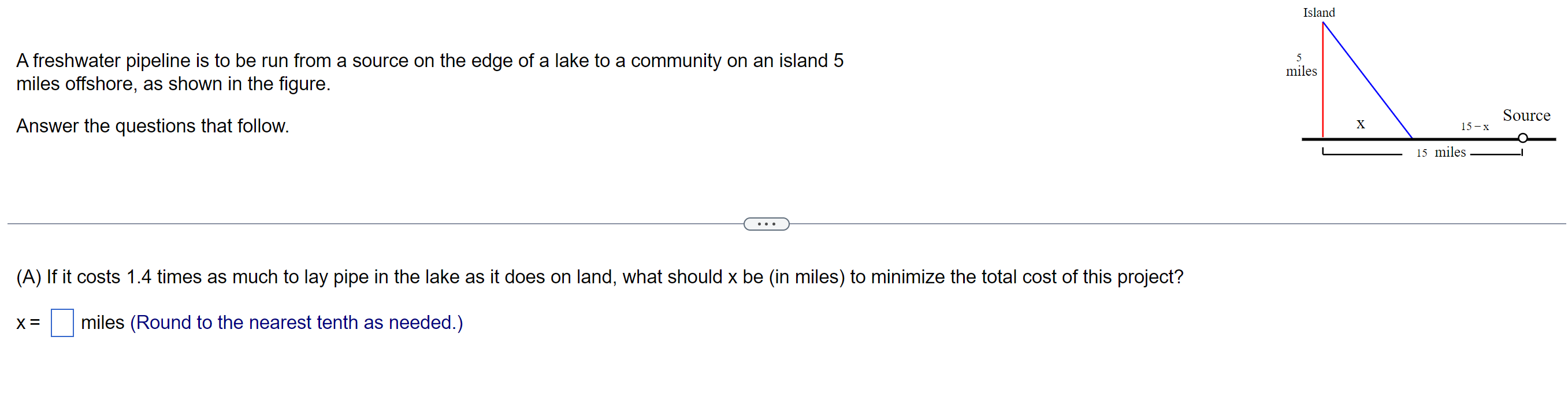
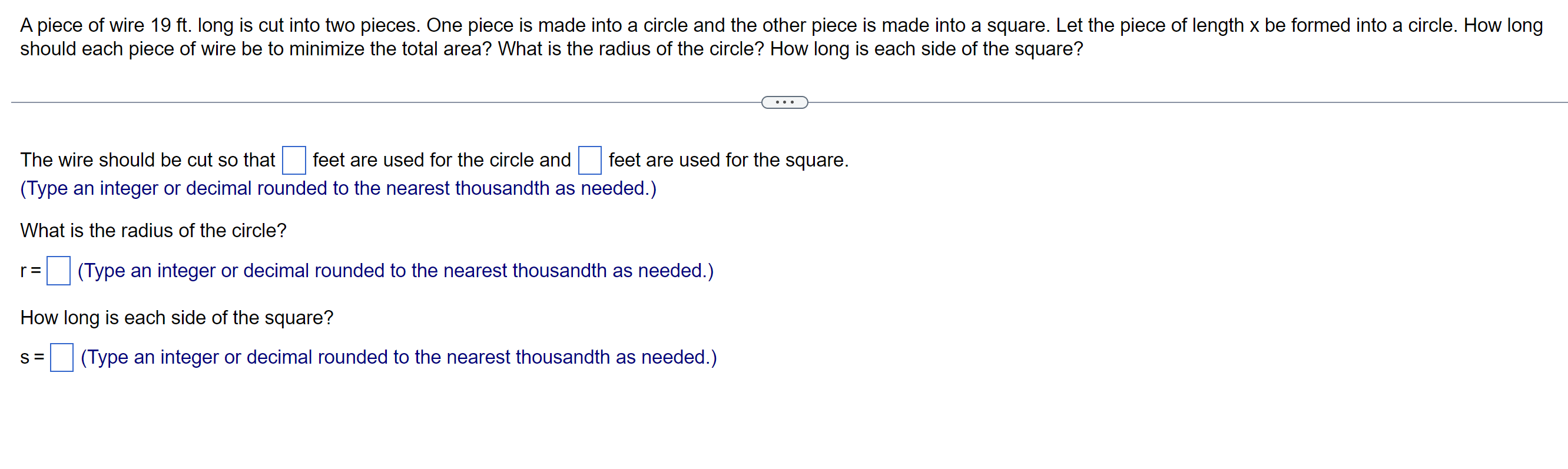
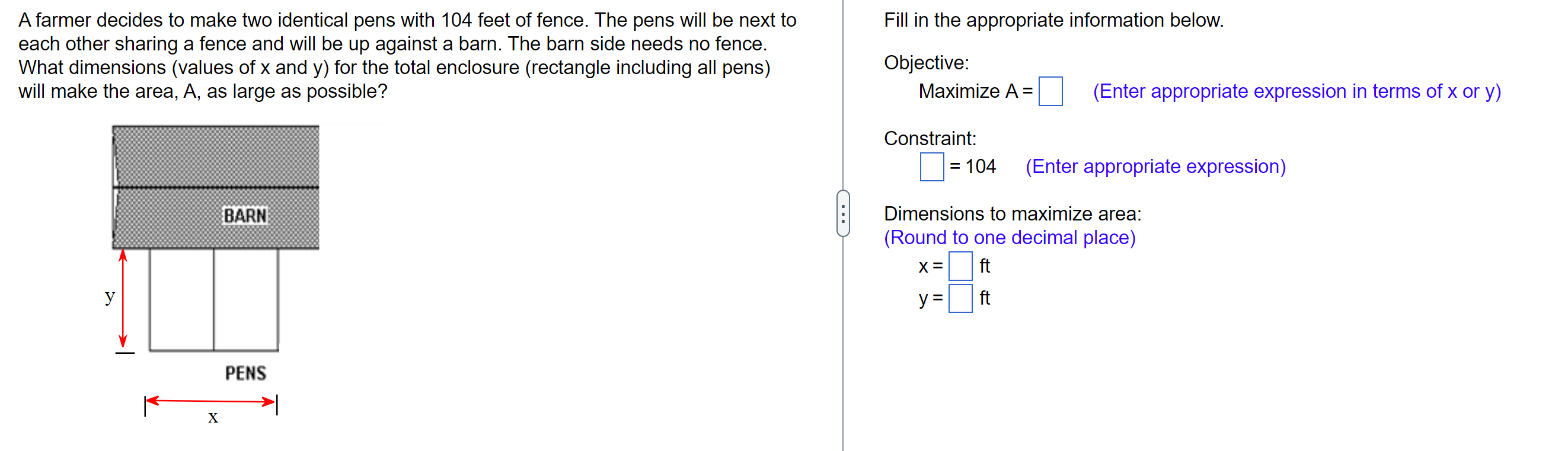
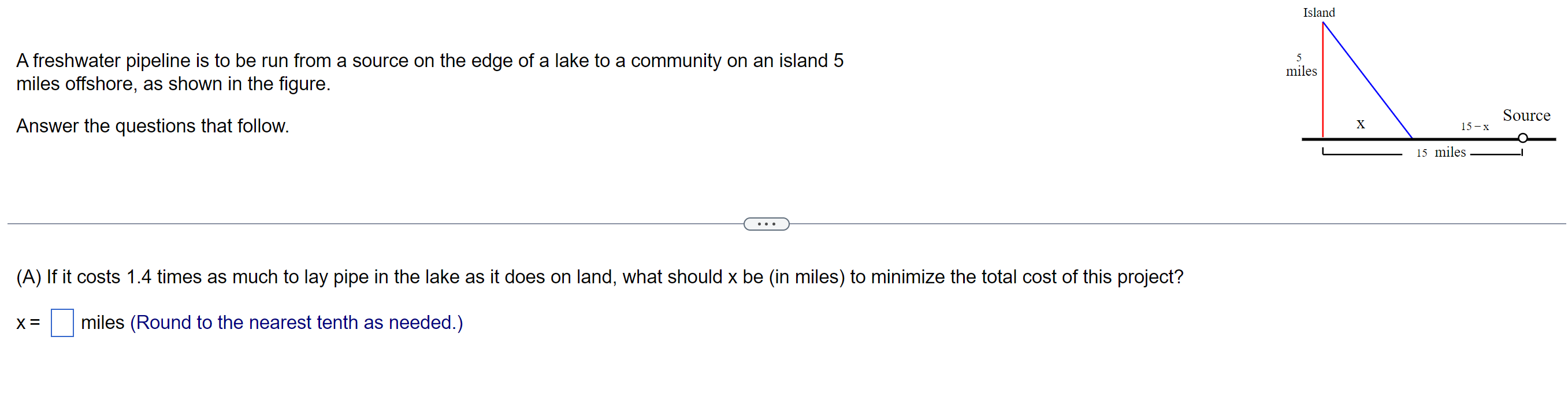
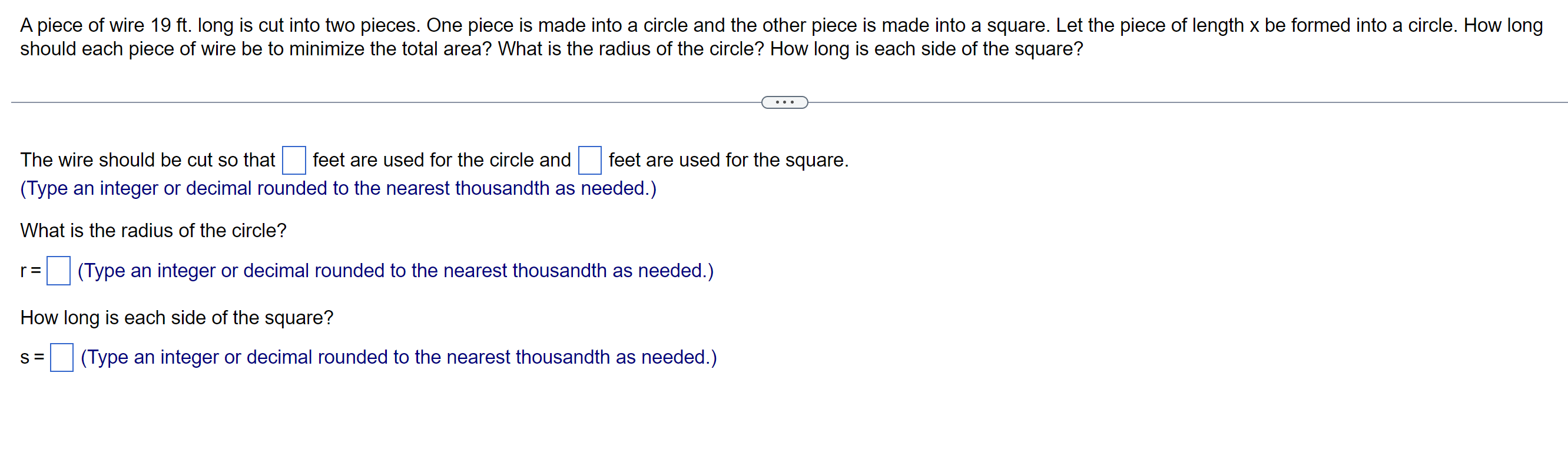
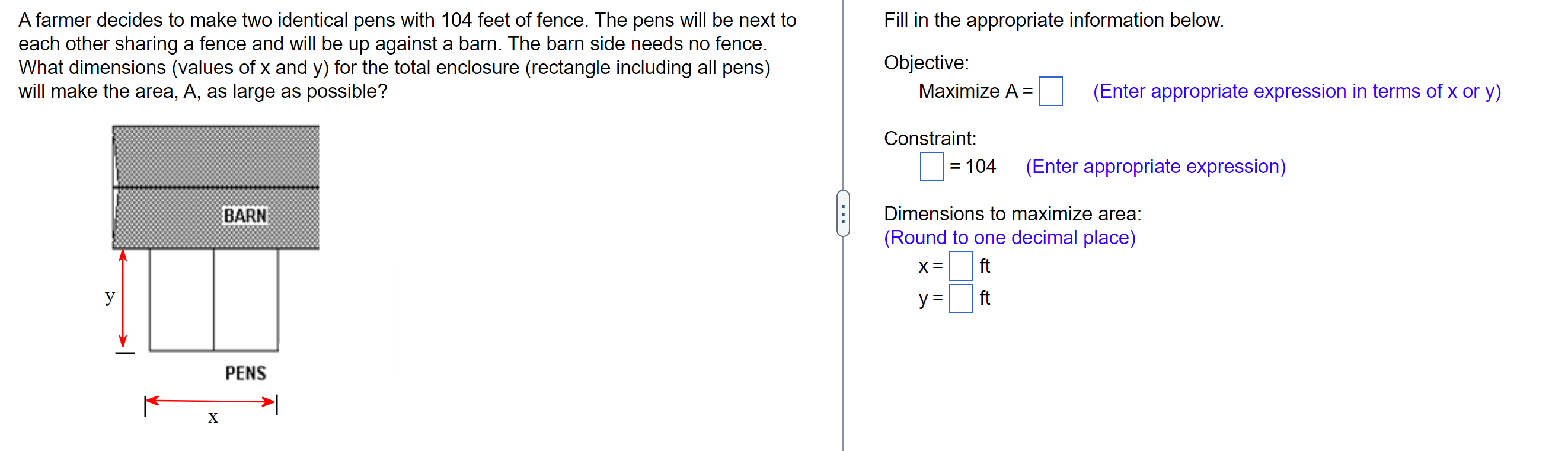
Developers from two towns, A and B, want to connect their towns to a highway. To minimize the cost of construction, the developers must find the City A location for the highway entrance that minimizes the total distance, d1 + d2, from the two towns to the highway. Let x be as shown. Find both the value of x that solves the developers' problem and the minimum total distance. City B miles Road Road niles X 24-x Highway 24 miles . . . What value of x minimizes the total distance? x = miles (Round to 1 decimal place.) What is the minimum total distance? miles (Round to 1 decimal place.)Island A freshwater pipeline is to be run from a source on the edge of a lake to a community on an island 5 miles miles offshore, as shown in the figure. Answer the questions that follow. Source 15 -x 15 miles . . . (A) If it costs 1.4 times as much to lay pipe in the lake as it does on land, what should x be (in miles) to minimize the total cost of this project? x = miles (Round to the nearest tenth as needed.)A fence is to be built to enclose a rectangular area of 1250 square feet. The fence along three sides is to be made of material that costs $4 per foot. The material for the fourth side costs $12 per foot. Find the dimensions of the rectangle that will allow for the most economical fence to be built. The short side is ft and the long side is ft.Starting with a 140-foot-long stone wall, a farmer would like to construct a rectangular enclosure by adding 560 feet of fencing, as shown in the figure to the right. Find the values of x and w that result in the greatest possible area. - X 140 feet W . . . X = ft W= ftA piece of wire 19 ft. long is cut into two pieces. One piece is made into a circle and the other piece is made into a square. Let the piece of length x be formed into a circle. How long should each piece of wire be to minimize the total area? What is the radius of the circle? How long is each side of the square? . . . The wire should be cut so that feet are used for the circle and feet are used for the square. (Type an integer or decimal rounded to the nearest thousandth as needed.) What is the radius of the circle? r=(Type an integer or decimal rounded to the nearest thousandth as needed.) How long is each side of the square? s = (Type an integer or decimal rounded to the nearest thousandth as needed.)A farmer decides to make two identical pens with 104 feet of fence. The pens will be next to Fill in the appropriate information below. each other sharing a fence and will be up against a barn. The barn side needs no fence. What dimensions (values of x and y) for the total enclosure (rectangle including all pens) Objective: will make the area, A, as large as possible? Maximize A = (Enter appropriate expression in terms of x or y) Constraint: = 104 (Enter appropriate expression) BARN . . . Dimensions to maximize area: (Round to one decimal place) X = ft y y= ft PENS X