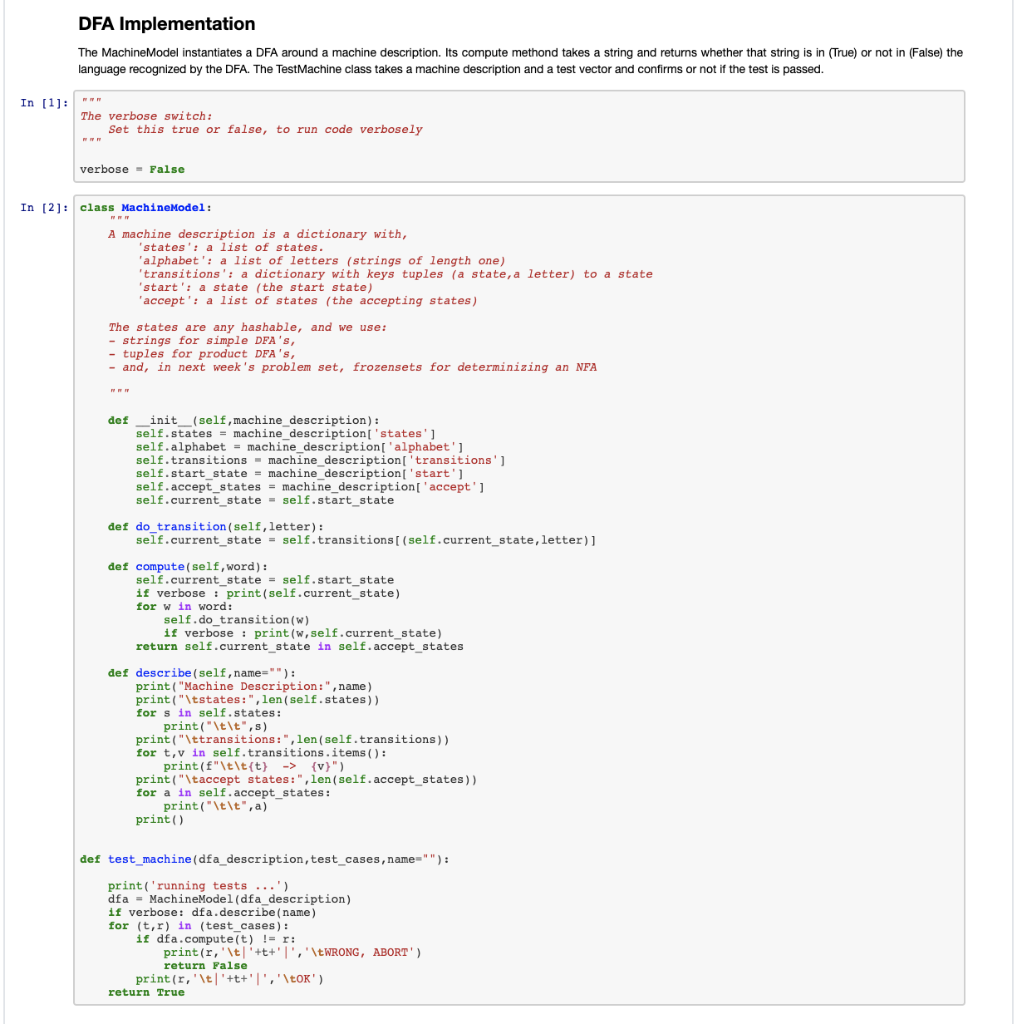
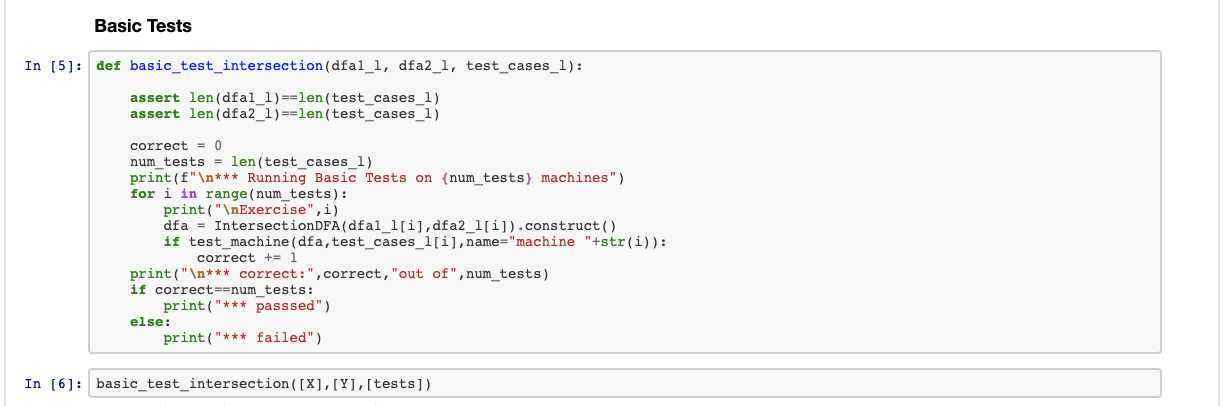
DFA Implementation The Machine Model instantiates DFA around a machine description. Its compute methond takes a string and returns whether that string is in (True) or not in (False) the language recognized by the DFA. The TestMachine class takes machine description and a test vector and confirms or not if the test is passed. In [1]: The verbose switch: Set this true or false, to run code verbosely verbose = False In [2]: class MachineModel: A machine description is a dictionary with, 'states': a list of states. 'alphabet': a list of letters (strings of length one) 'transitions': a dictionary with keys tuples (a state, a letter) to a state 'start': a state (the start state) 'accept': a list of states (the accepting states) The states are any hashable, and we use: strings for simple DFA'S, - tuples for product DFA's, - and, in next week's problem set, frozensets for determinizing an NFA det init__(self, machine_description): self.states = machine description('states'] self.alphabet = machine_description['alphabet'] self.transitions - machine_description['transitions'] self.start_state = machine_description('start' ] self.accept_states = machine_description['accept'] self.current_state = self.start_state def do_transition(self, letter): self.current_state = self. transitions[(self.current_state, letter)] def compute(self, word): self.current_state = self.start_state if verbose : print (self.current_state) for win word: self.do_transition(w) if verbose : print (w,self.current_state) return self.current_state in self.accept_states def describe (self,name=""): print("Machine Description:", name) print("\tstates:",len (self.states) for sin self.states: print("\t\t",s) print("\ttransitions:", len(self.transitions)) for t,v in self.transitions. items(): print("\t\t{t} -> {v}") print("\taccept states:", len(self.accept_states)) for a in self.accept_states: print("\t\t", a) print() def test_machine(dfa_description, test_cases, name=""): print('running tests ...') dfa - MachineModel(dfa_description) if verbose: dfa.describe (name) for (t,r) in (test_cases) : if dfa.compute(t) != r: print(r,'t'+t+'|', '\tWRONG, ABORT') return false print(r,'\t'+t+'l', 'OK') return True The Intersection Code The objective is to show that the intersection of two regular languages is regular. A DFA is easily complemented, so it is true that the intersection is regular by De Morgan's law, A AND B = NOT(NOT A OR NOT B). However the OR operation takes the two complemented DFA's and makes an NFA, which then has to be converted back to DFA's for the final complement. This can exponentiate the number of states. In this exercise we build a intersection machine directly. It is in the sprit of the NFA to DFA construction, in that we will simulate the computation of the two DFAs in parallel. We create product machine that has states form as pars. (s. 1), were is a state from the first machine, and t is a state from the second machine. To be in state (s, t) means that on the input used up to that moment in the computation, the first machine would be in states and the second in stater. There are several possibilities for the accepting states of a product machine, but to calculate the intersection of the two languages, a state (s. 1) is accepting in the product machine, ifs is accepting in the first machine and is accepting in the second mahince. Mathematical definition. Given two DFAS. , M;= (03, E, 8, 9j, 4.) i = 1, 2, the product machine m computing the intersection language (M)= (M) (M2). is given by the DFA, M = 0, XQ2, 2, 8, (91, 92), A, XA2), where : (, x,) Q. ((s, t), a) ( 8( a), 8(t, a)) In [3]: class IntersectionDFA: given two DFA descriptions, create a DFA description that accepts the intersection of the languages of the given DFA alphabets must be the same the two DFA's presented are in our standard form; the output DFA makes the change that states are 2-tuples of states. since tupes are immuatable, as are strings, this change does not affect any coding. output: 'states':list(tuple(string, string)) 'alphabet':list(character) 'transitions':dict(tuple(tuple(string, string), character): tuple(string, string) 'start': tuple(string, string) 'accept':list(tuple(string, string)) input: 'states':list(string) 'alphabet':list(character) 'transtions': dict(tuple(string, string):string) 'start':string 'accept':list(string) def __init__(self, dfal, dfa2): self.dfal - dfal self.dfa2 = dfa2 self.states - 01 self. alphabet = 0 self. transitions - {} self.start = None # an empty 2-tuple should go here, but those do not exist self.accept- # the alphabets must be the same assert set (dfall'alphabet']) == set (dfa2['alphabet']) def cartesian_product (self,11,12): given 11, 12 each a list(string), return the cartesian product list(tuple(string, string) of all pairs of strings, the first from the first list, the second from the second list pass #write code return None # replace None as well def do_transitions(self): create transitions of the Intersection DFA. - go through all state, letter pairs of the Intersection DFA - for each pair, refer to the transitions in dfal and dfa to find the resulting state in the Intersection DFA pass # write code def construct (self): construct the Intersection DFA. - what alphabet does it have - what start state does it have - what states does it have - what accept states does it have - what transitions does it have pass # write code return { states':self.states, 'alphabet':self.alphabet, 'transitions':self.transitions, 'start' :self.start, accept': self.accept } Simple test cases In [4]: # a sample machine X= 'states': [ 'xi', 'X2', '3', 'R'], 'alphabet':['a','b'], 'transitions: ('xl','b'):'xi',('xi', 'a'):'X2', ('X2','b'):'R', ('X2', 'a'):'X3', ('3', 'b') :'X3', ('X3', 'a'): 'R', ('R','a'): 'R',('R','b'):'R' } 'start':'xl', 'accept': [ 'X3'] } Y = { 'states': ['yl', 'Y2', 'Y3', 'R'), 'alphabet':['a','b'], 'transitions':{ ('Yl', 'a') :'71', ('Y','b'):'Y2', ('Y2', 'a'): 'R', ('Y2', 'b'): 'Y3', ('43', 'a') :'73, ('3','b'):'R', ('R','a': 'R', ('R','b'):'R' }, 'start':'Yl', 'accept':['13') } # a sample test tests=0 ('aabb', True), ('aabb', True), ('',False), ('a',False), ('b',False), ('bbbaa', False), ('aabbb',False) 1 * want verbose verbose = True test_machine (IntersectionDFA (X,Y).construct(), tests) # further testing ... Basic Tests In [5]: def basic_test_intersection (dfal_l, dfa2_1, test_cases_l): assert len(dfal_l)==len (test_cases_l) assert len(dfa2_1)==len (test_cases_l) correct = 0 num_tests = len(test_cases_l) print(f" *** Running Basic Tests on {num_tests} machines") for i in range(num_tests): print(" Exercise", i) dfa = IntersectionDFA(dfa1_l[i],dfa2_1[i]).construct() if test_machine (dfa, test cases_1[i], name="machine "+str(i)): correct += 1 print(" *** correct:",correct, "out of", num_tests) if correct==num_tests: print("*** passsed") else: print("*** failed") In [6]: basic_test_intersection([X],[Y],[tests]) DFA Implementation The Machine Model instantiates DFA around a machine description. Its compute methond takes a string and returns whether that string is in (True) or not in (False) the language recognized by the DFA. The TestMachine class takes machine description and a test vector and confirms or not if the test is passed. In [1]: The verbose switch: Set this true or false, to run code verbosely verbose = False In [2]: class MachineModel: A machine description is a dictionary with, 'states': a list of states. 'alphabet': a list of letters (strings of length one) 'transitions': a dictionary with keys tuples (a state, a letter) to a state 'start': a state (the start state) 'accept': a list of states (the accepting states) The states are any hashable, and we use: strings for simple DFA'S, - tuples for product DFA's, - and, in next week's problem set, frozensets for determinizing an NFA det init__(self, machine_description): self.states = machine description('states'] self.alphabet = machine_description['alphabet'] self.transitions - machine_description['transitions'] self.start_state = machine_description('start' ] self.accept_states = machine_description['accept'] self.current_state = self.start_state def do_transition(self, letter): self.current_state = self. transitions[(self.current_state, letter)] def compute(self, word): self.current_state = self.start_state if verbose : print (self.current_state) for win word: self.do_transition(w) if verbose : print (w,self.current_state) return self.current_state in self.accept_states def describe (self,name=""): print("Machine Description:", name) print("\tstates:",len (self.states) for sin self.states: print("\t\t",s) print("\ttransitions:", len(self.transitions)) for t,v in self.transitions. items(): print("\t\t{t} -> {v}") print("\taccept states:", len(self.accept_states)) for a in self.accept_states: print("\t\t", a) print() def test_machine(dfa_description, test_cases, name=""): print('running tests ...') dfa - MachineModel(dfa_description) if verbose: dfa.describe (name) for (t,r) in (test_cases) : if dfa.compute(t) != r: print(r,'t'+t+'|', '\tWRONG, ABORT') return false print(r,'\t'+t+'l', 'OK') return True The Intersection Code The objective is to show that the intersection of two regular languages is regular. A DFA is easily complemented, so it is true that the intersection is regular by De Morgan's law, A AND B = NOT(NOT A OR NOT B). However the OR operation takes the two complemented DFA's and makes an NFA, which then has to be converted back to DFA's for the final complement. This can exponentiate the number of states. In this exercise we build a intersection machine directly. It is in the sprit of the NFA to DFA construction, in that we will simulate the computation of the two DFAs in parallel. We create product machine that has states form as pars. (s. 1), were is a state from the first machine, and t is a state from the second machine. To be in state (s, t) means that on the input used up to that moment in the computation, the first machine would be in states and the second in stater. There are several possibilities for the accepting states of a product machine, but to calculate the intersection of the two languages, a state (s. 1) is accepting in the product machine, ifs is accepting in the first machine and is accepting in the second mahince. Mathematical definition. Given two DFAS. , M;= (03, E, 8, 9j, 4.) i = 1, 2, the product machine m computing the intersection language (M)= (M) (M2). is given by the DFA, M = 0, XQ2, 2, 8, (91, 92), A, XA2), where : (, x,) Q. ((s, t), a) ( 8( a), 8(t, a)) In [3]: class IntersectionDFA: given two DFA descriptions, create a DFA description that accepts the intersection of the languages of the given DFA alphabets must be the same the two DFA's presented are in our standard form; the output DFA makes the change that states are 2-tuples of states. since tupes are immuatable, as are strings, this change does not affect any coding. output: 'states':list(tuple(string, string)) 'alphabet':list(character) 'transitions':dict(tuple(tuple(string, string), character): tuple(string, string) 'start': tuple(string, string) 'accept':list(tuple(string, string)) input: 'states':list(string) 'alphabet':list(character) 'transtions': dict(tuple(string, string):string) 'start':string 'accept':list(string) def __init__(self, dfal, dfa2): self.dfal - dfal self.dfa2 = dfa2 self.states - 01 self. alphabet = 0 self. transitions - {} self.start = None # an empty 2-tuple should go here, but those do not exist self.accept- # the alphabets must be the same assert set (dfall'alphabet']) == set (dfa2['alphabet']) def cartesian_product (self,11,12): given 11, 12 each a list(string), return the cartesian product list(tuple(string, string) of all pairs of strings, the first from the first list, the second from the second list pass #write code return None # replace None as well def do_transitions(self): create transitions of the Intersection DFA. - go through all state, letter pairs of the Intersection DFA - for each pair, refer to the transitions in dfal and dfa to find the resulting state in the Intersection DFA pass # write code def construct (self): construct the Intersection DFA. - what alphabet does it have - what start state does it have - what states does it have - what accept states does it have - what transitions does it have pass # write code return { states':self.states, 'alphabet':self.alphabet, 'transitions':self.transitions, 'start' :self.start, accept': self.accept } Simple test cases In [4]: # a sample machine X= 'states': [ 'xi', 'X2', '3', 'R'], 'alphabet':['a','b'], 'transitions: ('xl','b'):'xi',('xi', 'a'):'X2', ('X2','b'):'R', ('X2', 'a'):'X3', ('3', 'b') :'X3', ('X3', 'a'): 'R', ('R','a'): 'R',('R','b'):'R' } 'start':'xl', 'accept': [ 'X3'] } Y = { 'states': ['yl', 'Y2', 'Y3', 'R'), 'alphabet':['a','b'], 'transitions':{ ('Yl', 'a') :'71', ('Y','b'):'Y2', ('Y2', 'a'): 'R', ('Y2', 'b'): 'Y3', ('43', 'a') :'73, ('3','b'):'R', ('R','a': 'R', ('R','b'):'R' }, 'start':'Yl', 'accept':['13') } # a sample test tests=0 ('aabb', True), ('aabb', True), ('',False), ('a',False), ('b',False), ('bbbaa', False), ('aabbb',False) 1 * want verbose verbose = True test_machine (IntersectionDFA (X,Y).construct(), tests) # further testing ... Basic Tests In [5]: def basic_test_intersection (dfal_l, dfa2_1, test_cases_l): assert len(dfal_l)==len (test_cases_l) assert len(dfa2_1)==len (test_cases_l) correct = 0 num_tests = len(test_cases_l) print(f" *** Running Basic Tests on {num_tests} machines") for i in range(num_tests): print(" Exercise", i) dfa = IntersectionDFA(dfa1_l[i],dfa2_1[i]).construct() if test_machine (dfa, test cases_1[i], name="machine "+str(i)): correct += 1 print(" *** correct:",correct, "out of", num_tests) if correct==num_tests: print("*** passsed") else: print("*** failed") In [6]: basic_test_intersection([X],[Y],[tests])