Dijkstra's Shortest Path Algorithm in Java

I need a NEW FRESH Java program. Not one that has been copied and pasted from another Chegg study question.

Implement Dijkstra's shortest path algorithm satisfying the following assumptions and requirements:

(a) The entire graph is not availabe in advance. The graph is implicity represented by the start vertex and a problem specfic "success(v)" function that gives for vertex v the set of "successor" nodes reachable by one edge from v. Some vertices represent a goal state.

(b) Maintain the expanded set E and the frontier set F in a suitable data structure that allows an efficient membership test (v E? v F?). In addition, F needs to support efficient priority queue operations.

(c) Edge costs may be negative, and hence a vertex in E may have to be moved to F.

(d) State representation, adjacency, and edge cost calculation must be easily modifiable to handle various problems such as:

"River-crossing" problems, such as The Missionaries and Cannibals: n missionaries and n cannibals are on one side of the river. How can they all cross the river, using a boat that can hold m people at a time, without every leaving more cannibals than missionaries on either side of the river at any time?

(e) Your program must output a path from the start vertex to the first goal vertex found (possibly backwards) and its cost. It should also output relevant statistics such as the number of vertices generated and the total CPU time.

Test your implementation on the following two sample problems:

(a) The weighted graph:

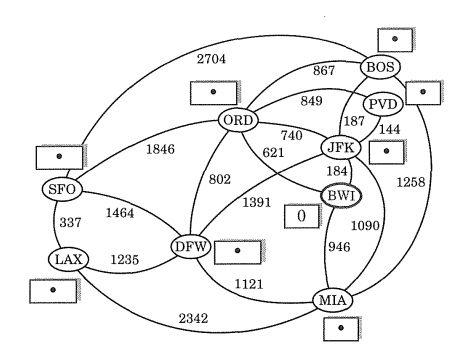
Assume BWI is the start vertex, and SFO and LAX are the goals. Your program must output a shortest cost path to SFO or LAX, whichever is closer to BWI.

(b) The Missionaries and Cannibals problem for the case n = 3 and m = 2, and for the case n = 4 and me = 3. Assume all edge costs are 1.

Please create:

A concise report describing the following:

1.) Implementation details of the data structures and methods for E and F.

2.) Details of the state and edge cost representations for the two sample problems.

3.) Test results (including the actual output) and a convincing argument of the correctness of the implementation.

4.) The source code

Please implement this in Java and include all source code. Including the set ups and test run outputs of the 2 sample problems defined.

Represent the graph, explored sets E and F, vertices, and edges however you wish.

Pseudo code to follow for core of algorithm:

E //this is the explored set

F {start node s} //this is the frontier set - the nodes that we have not yet generated successors of

g(s) 0

while F do

{

u min g-value node in F

if u is a goal

{

output path from u to s

}

F F - {u} //remove u from F (frontier set)

E E {u} //add u to E (explored set)

Expand u to generate successors u₁,...,u_k //this is where you call your success(v) function

for i 1 to k do

{

if u_i E and u_i F //first time seeing this node

{

g(u_i) g(u) + c(u, u_i) // c(x,y) computes and returns the cost from node x to node y

parent(u_i) u

F F {u_i} //add u_i to F

}

else if u_i F //found a better way to get to u_i through u

{

if g(u) + c(u, u_i) i)

{

g(u_i) g(u) + c(u, u_i)

parent(u_i) u

}

}

else if u_i E //to handle negative edge costs

{

if g(u) + c(u, u_i) i)

{

g(u_i) g(u) + c(u, u_i)

parent(u_i) u

E E - {u_i} //remove u_i from E

F F {u_i} //add u_i to F

}

}

} // end for

} // end while

2704 867 BOS 849 ORD PVD 187 A44 JFK 1846 621 184 802 1258 SFO BWI 1391 1464 337 1090 946 LAX 1235 1121 MIA. 2342