Discrete Math

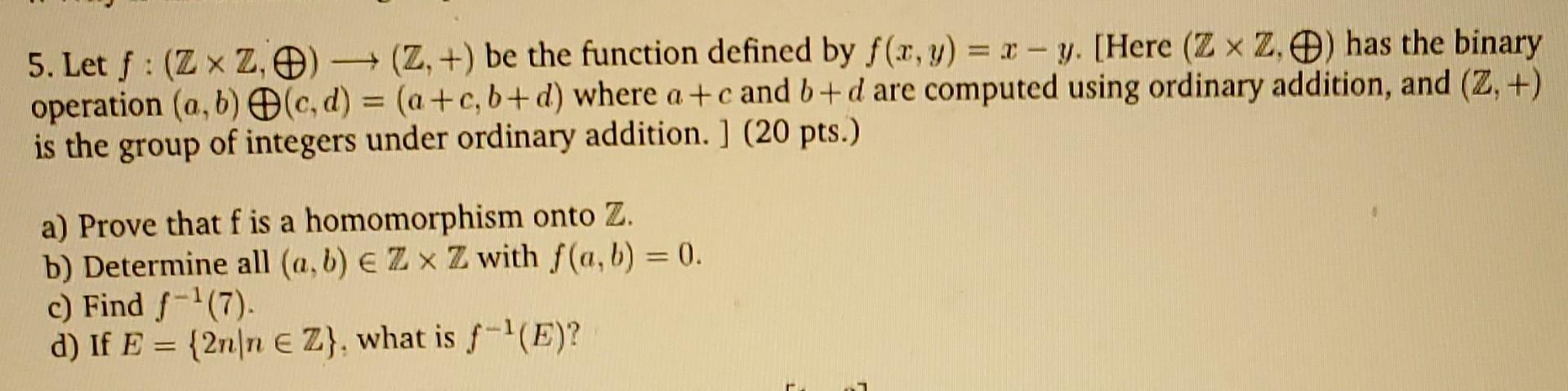
5. Let f:(ZZ,)(Z,+) be the function defined by f(x,y)=xy. [Here (ZZ,) has the binary operation (a,b)(c,d)=(a+c,b+d) where a+c and b+d are computed using ordinary addition, and (Z,+) is the group of integers under ordinary addition. ] ( 20pts.) a) Prove that f is a homomorphism onto Z. b) Determine all (a,b)ZZ with f(a,b)=0. c) Find f1(7). d) If E={2nnZ}, what is f1(E)