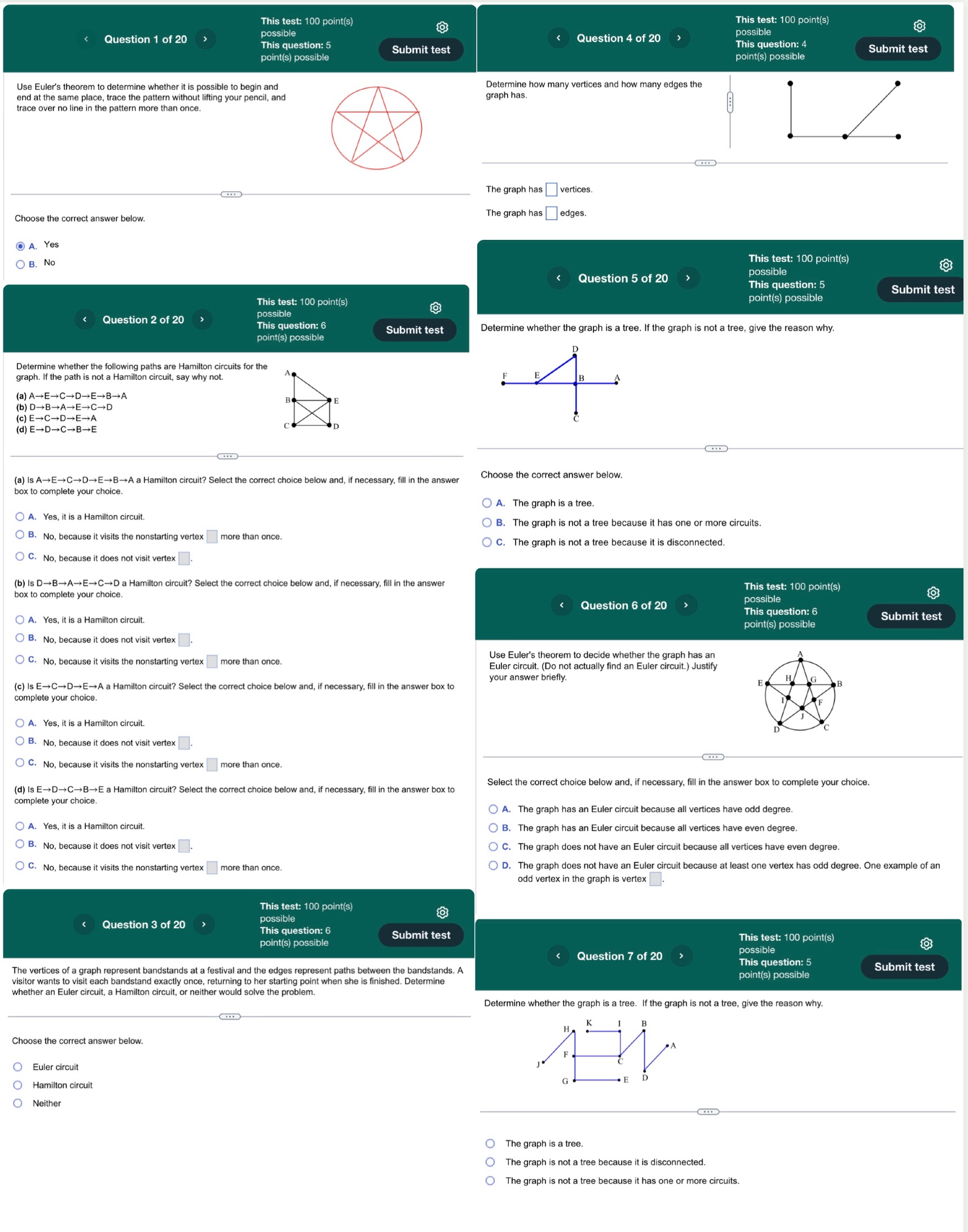
Question: Discrete Math Help! This test: 100 point(s) This test: 100 point(s) @ possible @ - possible - Question 1 of 20 g Question 4 of
Discrete Math Help!
This test: 100 point(s) This test: 100 point(s) @ possible @ - possible - Question 1 of 20 g Question 4 of 20 3 e This que 5 Submit test RS L Submit test point(s) possible point(s) possible Use Euler's theorem to determine whether it is possible to begin and Determine how many vertices and how many edges the end at the same place, trace the pattern without lifting your pencil, and graph has trace over no line in the pattern more than once. o The graph has vertices. The graph has edges. Choose the correct answer below. @ A. Yes This test: 100 point(s) @ possible B. No Ul E This question: 5 . This test: 100 point(s) @ point(s) possible possible LTS T Submit test Determine whether the graph is a tree. If the graph is not a tree, give the reason why. point(s) possible Question 2 of 20 Determine whether the following paths are Hamilton circuits for the graph. If the path is not a Hamilton circuit, say why not. (a) AECDEBA 3 5 (b) DBAECD (c) E=CDEA C D (d) EDCBE (a) 1s AECDEB+A a Hamilton circuit? Select the comect choice below and, i necessary, fil in the answer 00se the comect answer below. box to complete your choice. () A. The graph is a tree. ) A. Yes, it is a Hamilton circuit. 5 i b 0 w () B. The graph is not a tree because it has one or more circuits. ) B. No, because it visits the nonstarting vertex | more than cnce. O C: 'The graph is Aot & tias bacauise It s discannactad () . No, because it does not visit vertex (b) Is D+BAECD a Hamilton circuit? Select the correct choice below and, if necessary, fill in the answer TR T R O RS T G)] box to complete your choice. possible @ Question 6 of 20 A : . This question: 6 e (0 A. Yes, itis a Hamilton circuit. point(s) possible ) B. No, because it does not visit vertex QO C. No, b it visits th i h Use Euler's theorem to decide whether the graph has an =5 HeiDeceuse Rvists Dienonstarting verie: i more Than onee: Euler circuit. (Do not actually find an Euler circuit.) Justify your answer briefly. (c) Is E=+C+DEA a Hamilton circuit? Select the correct choice below and, if necessary, fill in the answer box to complete your choice. J A. Yes, itis a Hamilton circuit. B. No, because it does not visit vertex Oc. No, because it visits the nonstarting vertex more than once. : o ) . s Select the correct choice below and, if necessary, fill in the answer box to complete your choice. (d) Is E-DCBE a Hamilton circuit? Select the correct choice below and, if necessary, fill in the answer box to complete your choice. _ (O A. The graph has an Euler circuit because all vertices have odd degree O A. Yes, itis a Hamilton circuit. (O B. The graph has an Euler circuit because all vertices have even degree. ) B. No, because it does not visit vertex . () . The graph does not have an Euler circuit because all vertices have even degree. C. No, because it visits the nonstarting vertex = more than once. (0 D. The graph does not have an Euler circuit because at least one vertex has odd degree. One example of an odd vertex in the graph is vertex This test: 100 point(s) @ possible This question: 6 Submit test point(s) possible Question 3 of 20 This test: 100 point(s) @ possible This question: 5 LT point(s) possible Question7 of 20 > The vertices of a graph represent bandstands at a festival and the edges represent paths between the bandstands. A visitor wants to visit each bandstand exactly once, returning to her starting point when she is finished. Determine whether an Euler circuit, a Hamilton circuit, or neither would solve the problem Determine whether the graph is a tree. If the graph is not a tree, give the reason why. Choose the correct answer below. Euler circuit Hamilton circuit O Neither The graph is a tree. The graph is not a tree because it is disconnected. The graph is not a tree because it has one or more circuits