discrete math

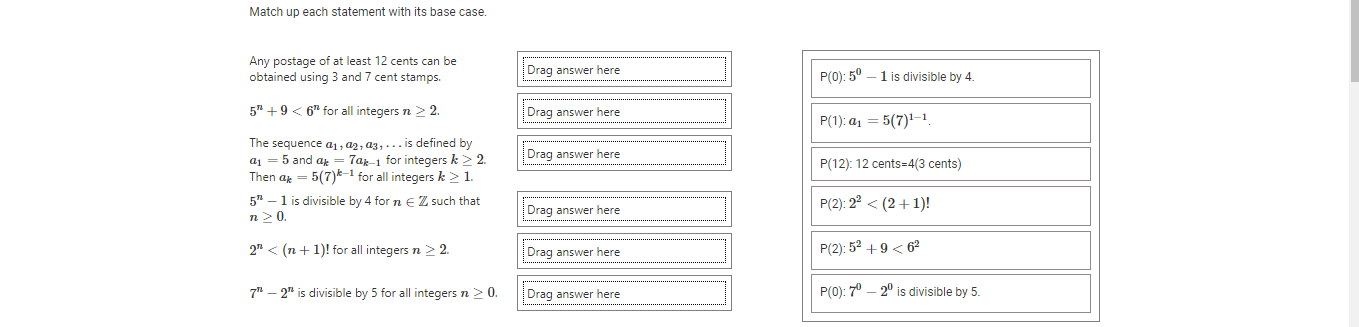
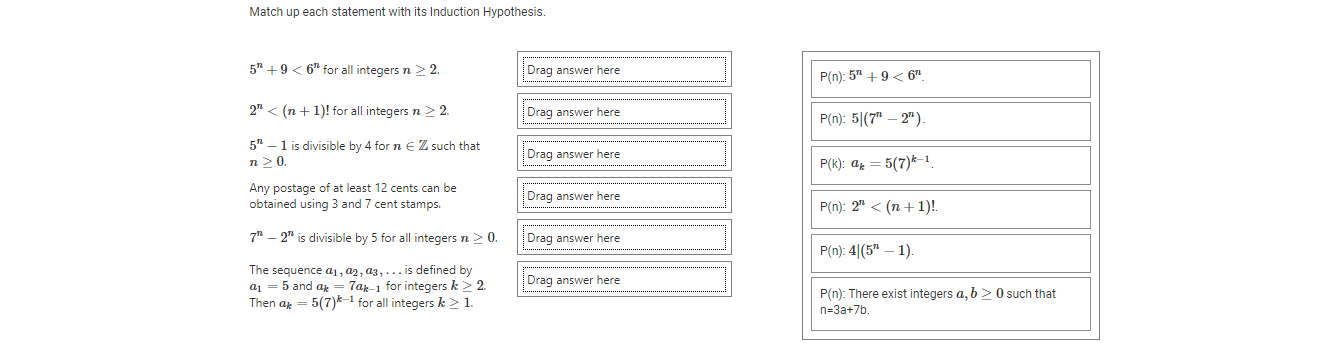
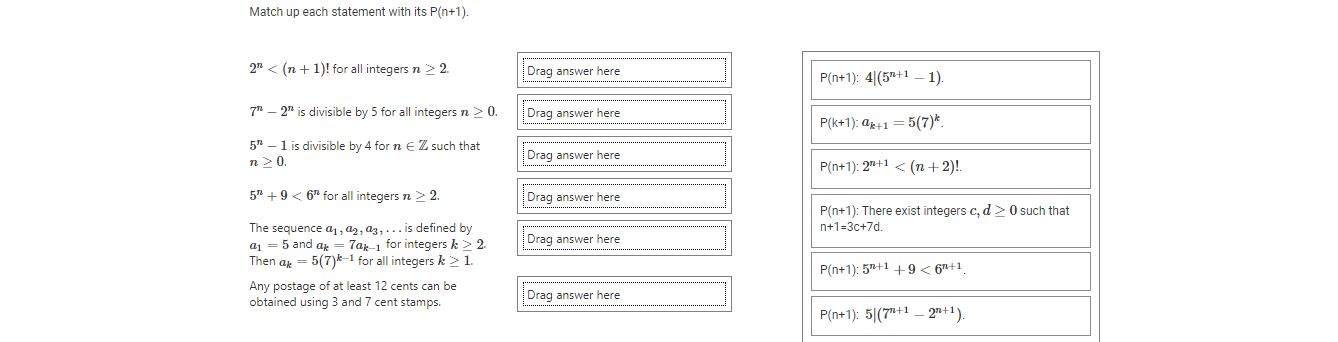
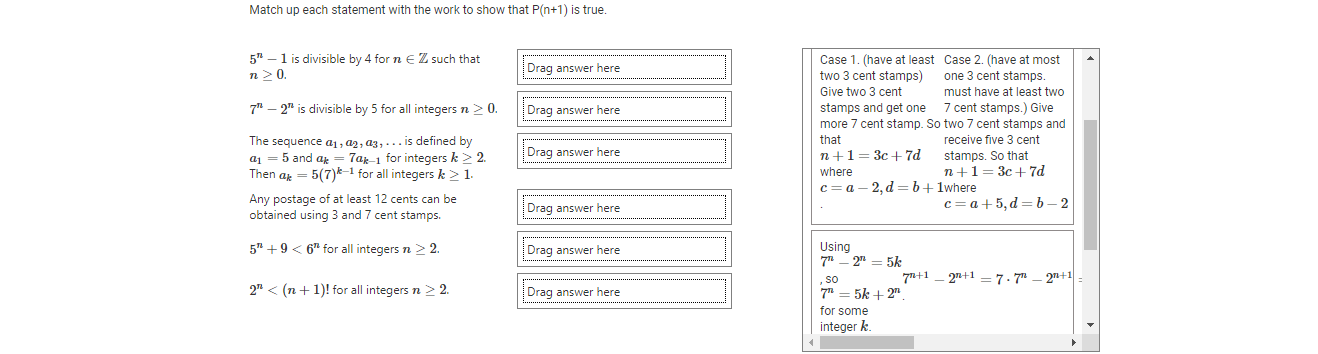
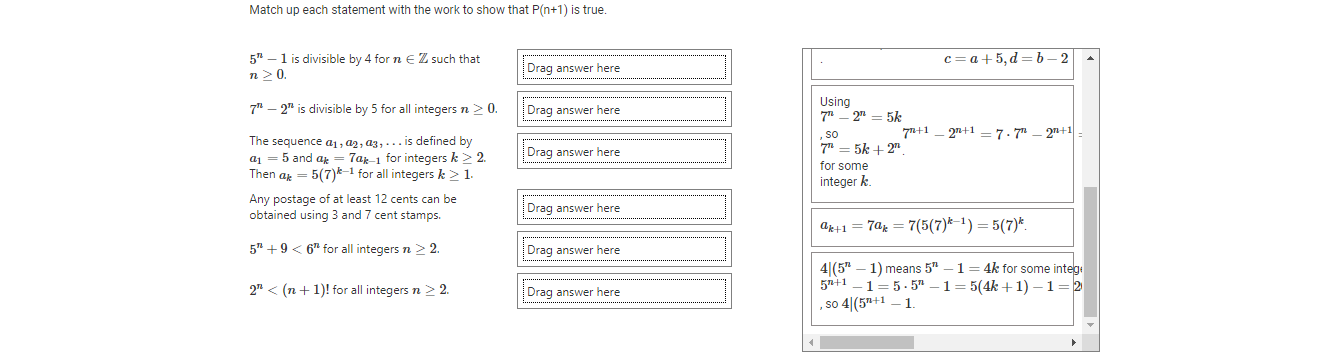
Match up each statement with its base case. Any postage of at least 12 cents can be obtained using 3 and 7 cent stamps. Drag answer here P(0): 50 - 1 is divisible by 4. 5" + 9 2 Drag answer here Then ap = 5(7)*-1 for all integers k 2 1. P(12): 12 cents=4(3 cents) 52 - 1 is divisible by 4 for n E Z such that P(2): 22 2. Drag answer here P(2): 52 + 9 0. Drag answer here P(0): 7" - 2" is divisible by 5.Match up each statement with its Induction Hypothesis. 5" + 9 2. Drag answer here P(n): 5" + 9 2. Drag answer here P(n): 5|(7" - 2" ) 5 - 1 is divisible by 4 for n E Z such that n 2 0. Drag answer here P(k): ak = 5(7)*-1 Any postage of at least 12 cents can be obtained using 3 and 7 cent stamps. Drag answer here P(n): 2" 0. Drag answer here P(n): 4(5" - 1). The sequence a1, a2, a3, . . . is defined by a1 = 5 and ax = 7ak-1 for integers k > 2. Drag answer here Then ak = 5(7)*-1 for all integers k 2 1. P(n): There exist integers a, b > 0 such that n=3a+7b.Match up each statement with its P(n+1). 2" 2. Drag answer here P(n+1): 4 (5 +1 - 1). 7 - 2" is divisible by 5 for all integers n 2 0. Drag answer here P(k+1): ak+1 = 5(7)* 5" - 1 is divisible by 4 for n E Z such that n 2 0. Drag answer here P(n+1): 2+1 2. Drag answer here P(n+1): There exist integers c, d > 0 such that The sequence a1, a2, ag, . . . is defined by n+1=3c+7d. a1 = 5 and ap = 7ap 1 for integers k > 2 Drag answer here Then ax = 5(7)*-1 for all integers k > 1. P(n+1): 5 +1 +9 2 Drag answer here n +1= 3c + 7d stamps. So that Then ak = 5(7)*-1 for all integers k > 1. where n +1 = 3c+7d Any postage of at least 12 cents can be c=a - 2, d = b+ 1where obtained using 3 and 7 cent stamps. Drag answer here c = a+5,d=b-2 5" + 9 2. Drag answer here Using - 20 = 5k SO 7 +1 2" 2. _2n+1 = 7 . 7" _ 2+1- Drag answer here 71 = 5k + 2" . for some integer k.Match up each statement with the work to show that P(n+1) is true. 5" - 1 is divisible by 4 for n E Z such that Drag answer here c= a+5,d=b-2 n 2 0. 7 - 2" is divisible by 5 for all integers n > 0. Drag answer here Using 71 _ 2" - 5k The sequence a1 , a2, a3, . . . is defined by SO 7+1 _ 2n+1 = 7. 7" _274+1- a1 = 5 and ap = 7ak_1 for integers k > 2. Drag answer here 7 - 5k + 2. Then ak = 5(7)*-1 for all integers k > 1. for some integer k. Any postage of at least 12 cents can be obtained using 3 and 7 cent stamps. Drag answer here ak+1 = 70k = 7(5(7)*-1) = 5(7)* 5" + 9 2. Drag answer here 4 (5 - 1) means 5" - 1 = 4k for some integ 2" 2. Drag answer here 52+1 - 1 = 5 .5" - 1 = 5(4k + 1) -1 = 2 , so 4 (57+1 - 1