Discrete math questions

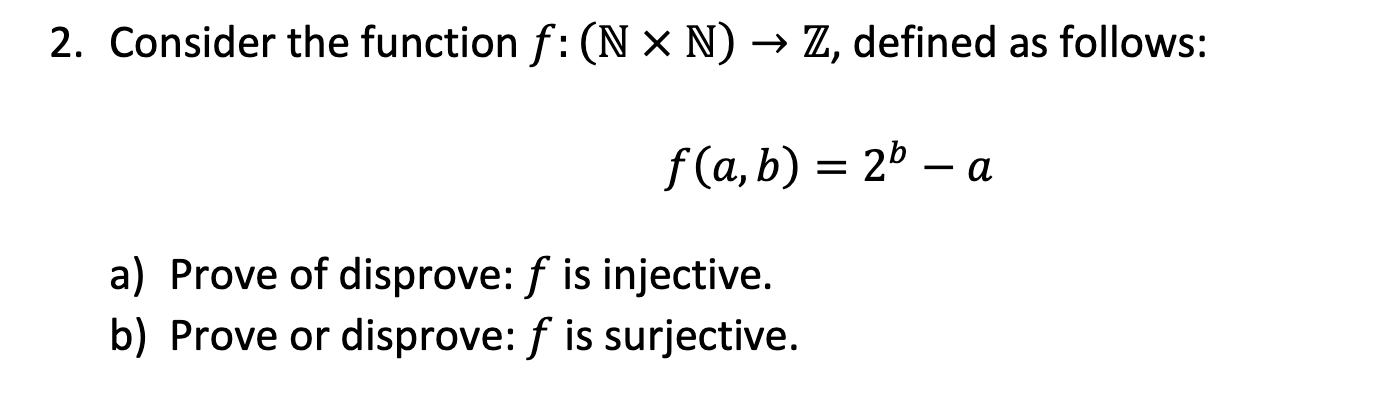
1. Let A, B, C be some (unknown) sets, and suppose that I have two functions f:A ) B and g: B > C which are known to be bijections. We define a third function, h: A > C to be the function defined by Mac) = g(f(x)). Prove that h is a bijection. 2. Consider the function f: (N X N) - Z, defined as follows: f(a, b) = 2b - a a) Prove of disprove: f is injective. b) Prove or disprove: f is surjective.3. Determine whether each of the following lists is: i) graphical ii) valid If yes, draw a corresponding graph to illustrate this. If no, give a reasonable explanation as to how you know this. a) {4-, 3,3,2,1,1,0} b) {3,2,1,1,1,1} c) {5,5,5,5,5,5} d) {5,4,4,2,2} e) {1,1,1,1,1,1,1,1} 4. Determine the Eulerization number of the following graph. Justify your answer by providing an Eulerization that adds the minimal number of edges. oooooo 5. Consider the complete bipartite graph K3'6. Is this graph Hamiltonian? Explain your reasoning by either drawing a Hamiltonian cycle, or giving a reasonable argument why such a cycle does not exist. 6. What is the chromatic number of the following graph? Provide a colouring to support your answer, and explain how you know that this is the least number of colours that allows for a proper colouring of this graph. 7. Let G be a graph with n vertices. Prove that at least two of the vertices of G must have the same degree