Discrete mathematics problem, I do not know how to solve both of these problems, I have been at it for hours.

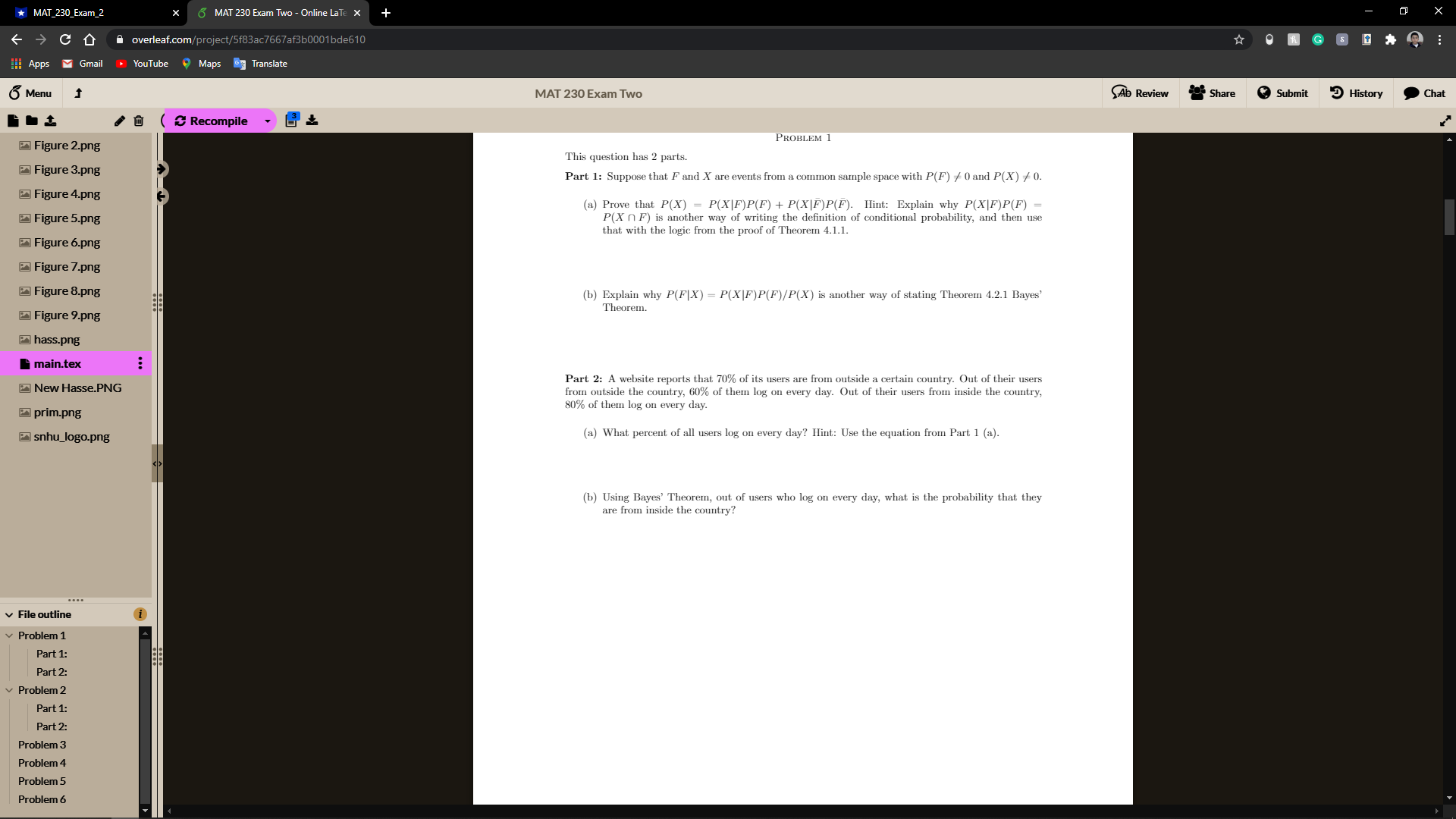
*MAT_230_Exam_2 6 MAT 230 Exam Two - Online La Te X C D overleaf.com/project/5f83ac7667af360001bde610 9 GS 1# lli Apps M Gmail YouTube 9 Maps Translate 6 Menu MAT 230 Exam Two Ab Review Share Submit History Chat &Recompile Figure 2.png PROBLEM 1 This question has 2 parts. Figure 3.png Part 1: Suppose that F and X are events from a common sample space with P(F) / 0 and P(X) / 0. Figure 4.png (a) Prove that P(X) = P(X|F)P(F) + P(X|F)P(F). Hint: Explain why P(X|F) P(F) = Figure 5.png P(X n F) is another way of writing the definition of conditional probability, and then use that with the logic from the proof of Theorem 4.1.1. Figure 6.png Figure 7.png Figure 8.png (b) Explain why P(FIX) = P(X|F)P(F)/P(X) is another way of stating Theorem 4.2.1 Bayes' Figure 9.png Theorem. hass.png i main.tex New Hasse.PNG Part 2: A website reports that 70% of its users are from outside a certain country. Out of their users from outside the country, 60% of them log on every day. Out of their users from inside the country, prim.png 80% of them log on every day. snhu_logo.png (a) What percent of all users log on every day? Hint: Use the equation from Part 1 (a). (b) Using Bayes' Theorem, out of users who log on every day, what is the probability that they are from inside the country? v File outline i Problem 1 Part 1: Part 2: Problem 2 Part 1: Part 2: Problem 3 Problem 4 Problem 5 Problem 6