(Discrete Structures): The Fibonacci sequence is defined as follows:

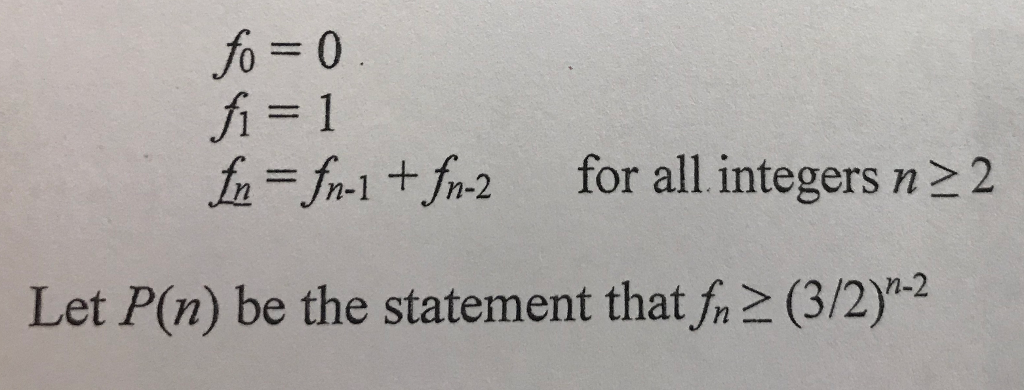
In this problem, we will use strong induction to prove that P(n) is true for all n > 0.

a. Show that the base cases P(1) and P(2) are true.

b. For any k 2, what is the inductive hypothesis? (Remember we're using strong induction!)

c. Show that the inductive hypothesis implies P(k+1).

n = -1 + fn-2 for all integers n 2 Let P(n) be the statement that fn2 (3/2) 2