Discuss the indifference curve for perfect substitutes

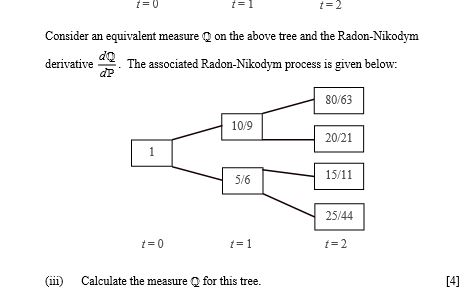
1 Let P be a probability measure equivalent to a different probability measure Q on a non-recombinant binomial tree. (1) Define the Radon-Nikodym derivative of @ with respect to P over the time horizon , written as and with respect to a random variable ) defined on de the nodes of the tree. [4] (hi) Explain the purpose of the Radon-Nikodym derivative and how it can be used in option pricing. [2] Consider a stochastic process that evolves in discrete time ? according to a binomial tree. The set of possible values of the process are shown below for ? = 0, 1 and 2, together with a probability measure P. 1/2 90 3/5 70 1/2 65 50 1/3 40 70 2/5 2/3 20 1=0 1 =1 1=2Consider an equivalent measure ( on the above tree and the Radon-Nikodym derivative dQ The associated Radon-Nikodym process is given below: aP 80/63 10/9 20/21 5/6 15/11 25/44 1=0 1 =1 1=2 (ii) Calculate the measure @ for this tree. [4]2 (1) Describe the following interest rate derivatives: (a) an interest rate floor (b) an interest rate floorlet (c ) a plain vanilla swap (d) ( e ) a European receiver swaption a forward rate agreement [5] A financial institution has committed to paying one of its clients a minimum rate of Interest of 3% p.a. convertible half yearly and payable half yearly on an agreed notional for five years, starting in five years' time. At that point (ie. in five years' time), the client chooses whether to receive this guaranteed 3% p.a. throughout the next five years or to earn LIBOR on the notional amount. (ii) Discuss the effectiveness of the financial institution attempting to hedge out the guarantee, focussing on the interest rate implications only, using each of the following: (a) a 3% p.a. five-year interest rate floor, starting in five years' time (b) ten floorlets to pay 1.5% over the six month periods ending at times 5.5, 6, 6.5, ..., 10 (c) a swaption to enter into a swap to receive 3% p.a. for five years starting in five years' time (d) a five year call option to buy a five-year 3% p.a coupon bond in five years' time (e) a forward rate agreement to earn 3% p.a. over five years, starting in five years' time and expected to be cash settled in five years' time [For parts (a), (c), (d) and (e) the 3% p.a. is convertible and payable half- yearly.] [7]3 Suppose that, in a developed market, the most popular caps have reset times f = 1, 2, 3, . (in years). A company which operates within that market is developing and calibrating a LIBOR. Market Model (LMM) to use for pricing interest rate derivatives. Define the following notation: . F(() = forward rate between times & and #+1 as seen at time t, annually compounded . 5(0 = volatility of F:(1) at time t . v.(1) = volatility of the zero-coupon bond price F(t,*) at time : . P(:,*) = price at time f of zero-coupon bond with principal 1 maturing at time k. You may assume that: F (D) = ((0)[ving(0 - vei(0]F (t)di + ((OF,()d in the rolling forward risk-neutral world, where int(() is the smallest integer such that int(f) > f (ie. it is the time of the next reset). (i) Define the rolling forward risk-neutral world. [1] (ii) Show that: v:(D) - VH1(D) = FOOL(O/(1+F(D) by applying Ito's lemma to InP(t,() - In(F(t,#+1) = In(1+F(0). [4] (iii) Derive an expression for aF (() in terms of the forward rate volatilities in the rolling forward risk-neutral world, using the result from part (ii). [5]Suppose now that ( (() is only a function of the number of whole years between the next reset date and time k. So Cr(() = At int(b- On a particular day, the Black volatilities of a series of one-year caplets are as follows: Year LAG 4 Black volatility 15% 18% 18% 18% 17% (iv) Derive the Ag, Aj, .., Aq parameters necessary to calibrate the LMM. [4]