Distribution normality samples.

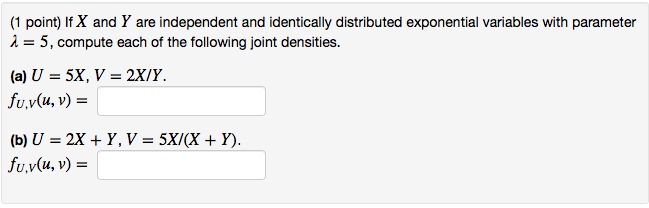
Final exam scores for an introductory statistics course follow a normal distribution with a mean p = 80 points and a standard deviation of a = 7.5 points. This course serves as a prerequisite for an advanced statistics class and students can only take the advanced course if they have earned a 73 or above on the final examination, a) What percent of test takers qualify for the advanced course? b) What is the probability that a randomly selected student in the introductory course qualifies for the advanced course? c) What is the probability that a class of n = 25 students (assume classes are randomly assigned) has an average score of 73 or above on the final exam?(1 point) If X and Y are independent and identically distributed exponential variables with parameter 1. = 5, compute each of the following joint densities. (a) U = 5X, V = 2X/Y. fu,v(u, v) = (b) U = 2X + Y, V = 5X/(X + Y). fu,v(u, v) =0 Fall Main (SUBR) - Advanced Statistics (PSYC-277 The average rested worker at a calculator production plant can assemble 106 pocket calculators an hour. During the last hour of their shift, 26 workers assemble an average of 97.4 calculators, with s = 17.2, Is the investigator correct in his assumption that the performance of these workers is significantly worse at the end of the shift? The investigator decides on a level of 5% for inferring the operation of nonchance factors. The appropriate null hypothesis, Ho, for this problem is4. (10pts) Let X1, X2, ... be i.i.d Uniform(0,1) and X() and X(n) are the smallest and largest order statistics. Show that (X(n) - X(1)| -> 1 (Do not use the following argument unless you prove it : If Xn > X and Yn ) Y, then Xn - Yn - X - Y. Instead use the definition of convergence in probability.)