Do e

Do c, e, g

Do b

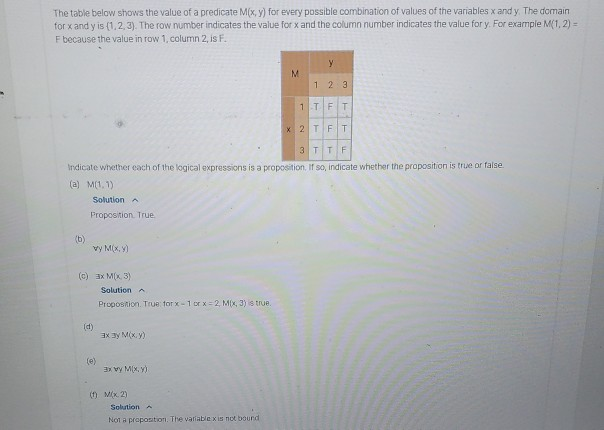
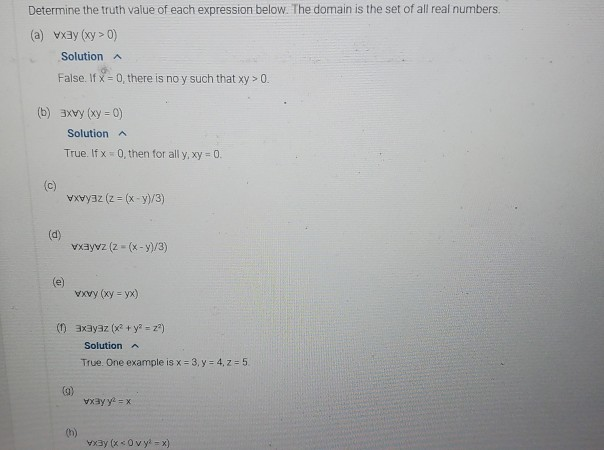
The table below shows the value of a predicate Mix,y) for every possible combination of values of the variables x and y. The domain for x and yis (1.2.3). The row number indicates the value for x and the column number indicates the value for y. For example M{1, 2) = Fbecause the value in row 1 column 2 is F. Indicate whether each of the logical expressions is a proposition. If so, indicate whether the proposition is true or false (a) M(1.1) Solution Proposition True vy MIX) (c) ax MIX 3) Solution Pico True Tot 10x_2 Mix, 3) s true x y Mix " vy Mix) W Solution Not a proposition. The variablexis not bound Determine the truth value of each expression below. The domain is the set of all real numbers. (a) vxay (xy > 0) Solution False. If x = 0, there is no y such that xy > 0. b) 3xvy (xy=0) Solution True. If x 0, then for all y, xy = 0. vxwy3z (z = (x - y)/3) vxayvz (z-(- y)/3) | vyvy (X) = y) (1) axayaz (x + y = z) Solution True. One example is x = 3, y = 4, z = 5 " Tayyi x way (x sovy= x) The domain for variables x and y is a group of people. The predicate F(x, y) is true if and only if x is a friend of y. For the purposes of this problem, assume that for any person x and person y, either x is a friend of y or x is an enemy of y. Therefore, -F(x,y) means that x is an enemy of y Translate each statement into a logical expression. Then negate the expression by adding a negation operation to the beginning of the expression. Apply De Morgan's law until the negation operation applies directly to the predicate and then translate the logical expression back into English (a) Everyone is a friend of everyone. Solution vx wy F(x, y) Negation VX vy F(x, y) Apply De Morgan's law ax ay -F(xy) English Someone is an enemy of someone Someone is a friend of someone Someone is a friend of everyone. Everyone is a friend of someone