Do NOT use single payment analysis.

this answer uses single payment analysis. please dont resubmit this formula

cash flow should have shifted time line

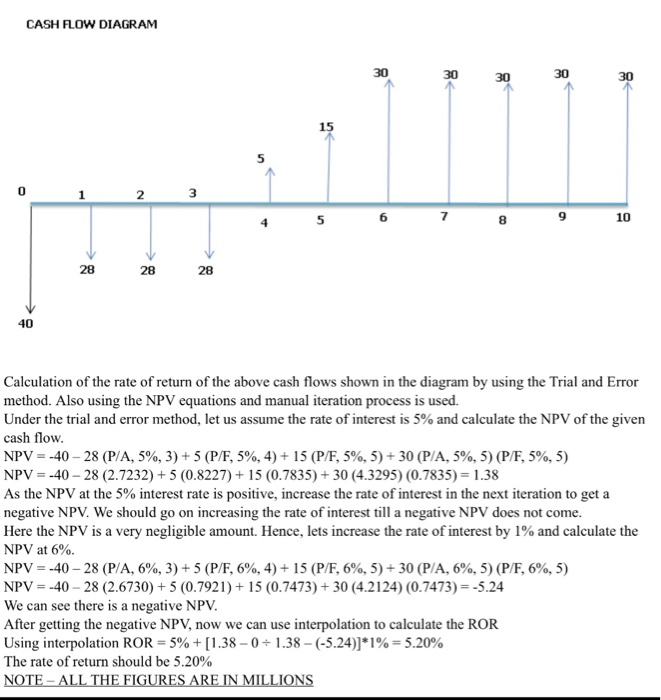
include cash flow diagram D4 NoTust SINGLE Anaysis An internet company projects the following cash flows shown in the table below (in millions). Using a Net Present Worth Balancing Equation and a manual iteration process compute the Rate of Return Cash Flow (millions) -40 Year 0 1-3 4 28 +15 +30 6-10 CASH FLOW DIAGRAMM 5 0 2 5 8 9 10 28 28 28 40 Calculation of the rate of return of the above cash flows shown in the diagram by using the Trial and Error method. Also using the NPV equations and manual iteration process is used. Under the trial and error method, let us assume the rate of interest is 5% and calculate the NPV of the given cash flow NPV--40-28 (PA, 5%, 3) + 5 (P/F, 5%, 4) + 15 (P/F, 5%, 5) + 30 (P/A, 5%, 5) (P/E 5%, 5) NPV--40- 28 (2.7232) +5 (0.8227)+15 (0.7835)+30 (4.3295) (0.7835 1.38 As the NPV at the 5% interest rate is positive, increase the rate of interest in the next iteration to get a negative NPV. We should go on increasing the rate of interest till a negative NPV does not come. Here the NPV is a very negligible amount. Hence, lets increase the rate of interest by 1% and calculate the NPV at 6%. NPV--40-28 (PA, 6%, 3) + 5 (PF. 6%, 4) +15 (P/E 6%, 5) + 30 (PA, 6%, 5) (P/F, 6%, 5) NPV--40 28 (2.6730) +5 (0.7921) + 15 (0.7473)+30 (4.2124) (0.7473)5.24 We can see there is a negative NPV After getting the negative NPV, now we can use interpolation to calculate the ROR Using interpolation ROR 5% + [1.38-0-1.38-(-5.24)]* 1%-5.20% The rate of return should be 5.20% include cash flow diagram D4 NoTust SINGLE Anaysis An internet company projects the following cash flows shown in the table below (in millions). Using a Net Present Worth Balancing Equation and a manual iteration process compute the Rate of Return Cash Flow (millions) -40 Year 0 1-3 4 28 +15 +30 6-10 CASH FLOW DIAGRAMM 5 0 2 5 8 9 10 28 28 28 40 Calculation of the rate of return of the above cash flows shown in the diagram by using the Trial and Error method. Also using the NPV equations and manual iteration process is used. Under the trial and error method, let us assume the rate of interest is 5% and calculate the NPV of the given cash flow NPV--40-28 (PA, 5%, 3) + 5 (P/F, 5%, 4) + 15 (P/F, 5%, 5) + 30 (P/A, 5%, 5) (P/E 5%, 5) NPV--40- 28 (2.7232) +5 (0.8227)+15 (0.7835)+30 (4.3295) (0.7835 1.38 As the NPV at the 5% interest rate is positive, increase the rate of interest in the next iteration to get a negative NPV. We should go on increasing the rate of interest till a negative NPV does not come. Here the NPV is a very negligible amount. Hence, lets increase the rate of interest by 1% and calculate the NPV at 6%. NPV--40-28 (PA, 6%, 3) + 5 (PF. 6%, 4) +15 (P/E 6%, 5) + 30 (PA, 6%, 5) (P/F, 6%, 5) NPV--40 28 (2.6730) +5 (0.7921) + 15 (0.7473)+30 (4.2124) (0.7473)5.24 We can see there is a negative NPV After getting the negative NPV, now we can use interpolation to calculate the ROR Using interpolation ROR 5% + [1.38-0-1.38-(-5.24)]* 1%-5.20% The rate of return should be 5.20%