do the problem 4.2.1, 4.2.2, 4.2.3

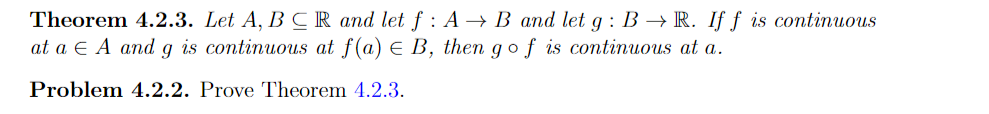
4.2 Pointwise Continuity Let A C R and consider f: A R. In the previous section, we talked about pointwise limits of f at limit points of A. Whenever is in the domain of f, i.e., when A, we can talk about whether the pointwise limit of f at is equal to the function evaluated at , i.e., we may ask whether lim, ,. f(z) = f(e). If it is so, then [ is called continuous at c A. Definition 4.2.1 (continuity). A function f: A R is called continuous at a A if for all > 0 there exists a 4 > 0 such that |t a|l 0}. Theorem 4.2.3. Let A, B C R and let f : A -> B and let g : B -> R. If f is continuous at a E A and g is continuous at f(a) E B, then go f is continuous at a. Problem 4.2.2. Prove Theorem 4.2.3.Problem 4.2.3 (Banach's fixed point theorem). Let f : R - R be a Lipschitz function with Lipschitz constant 0