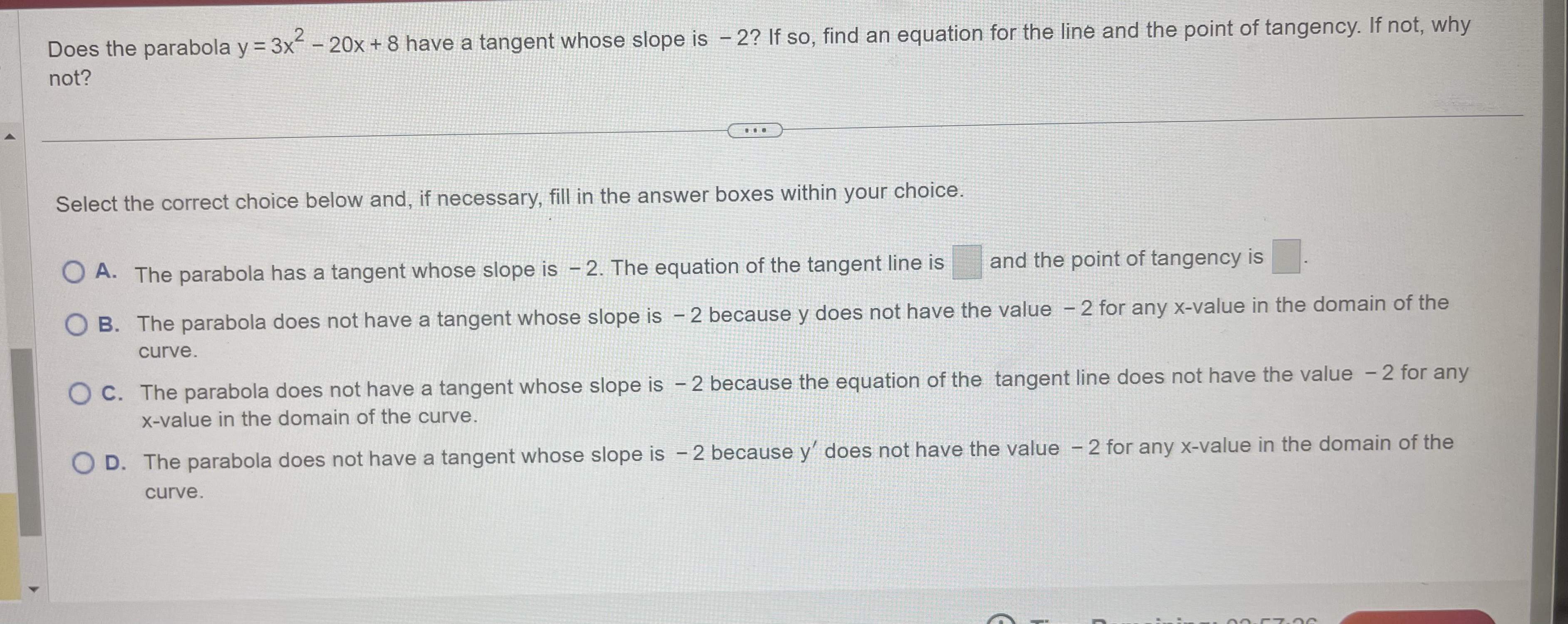
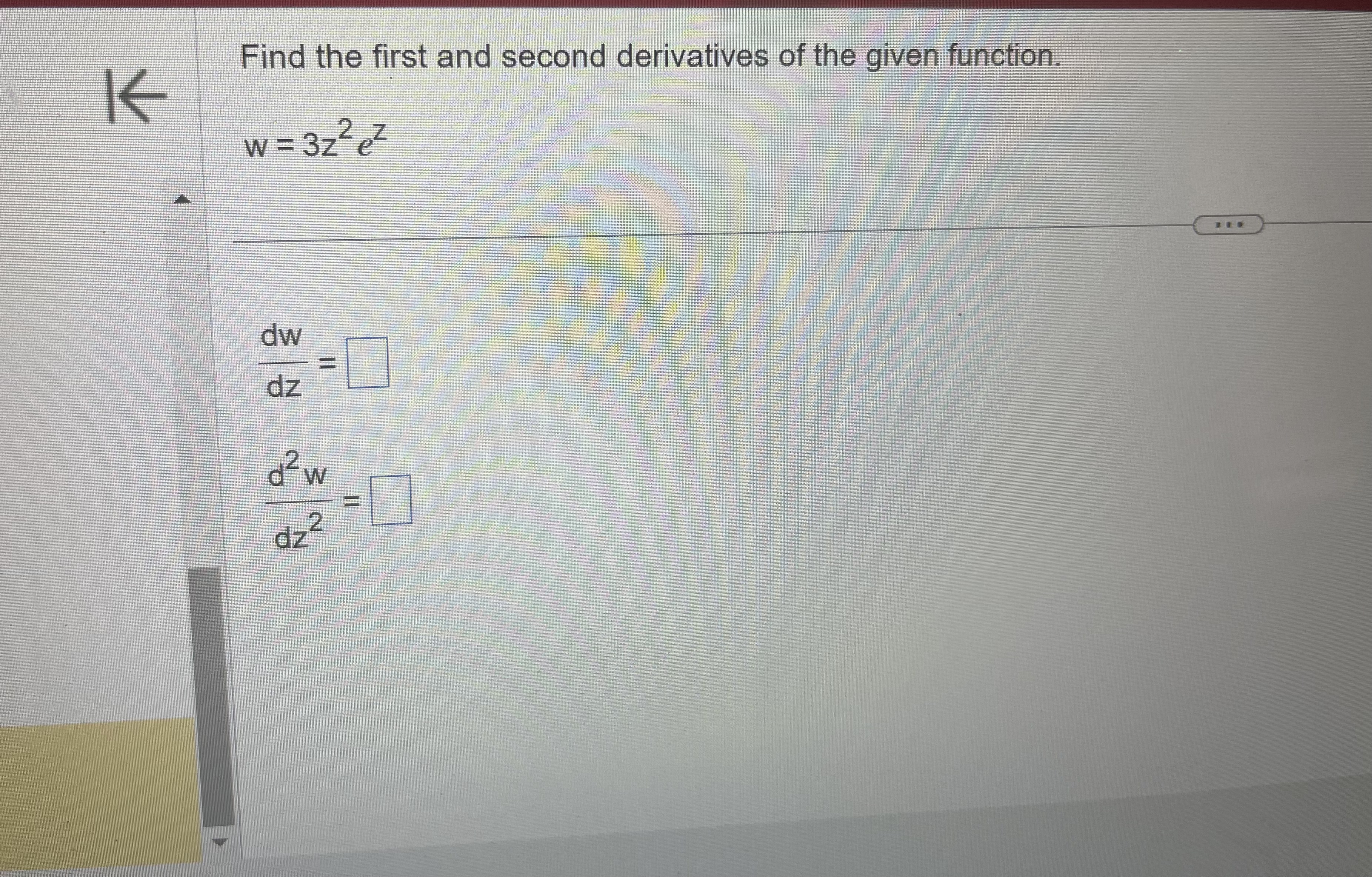
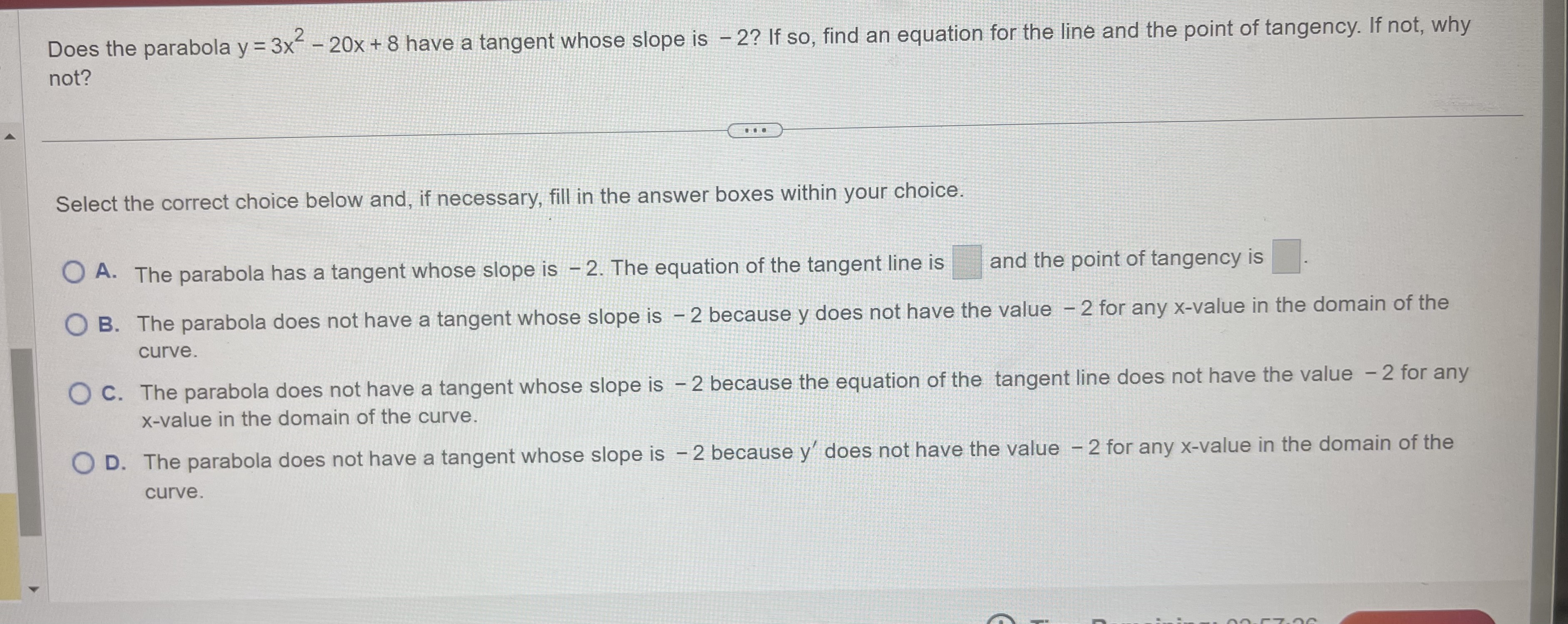
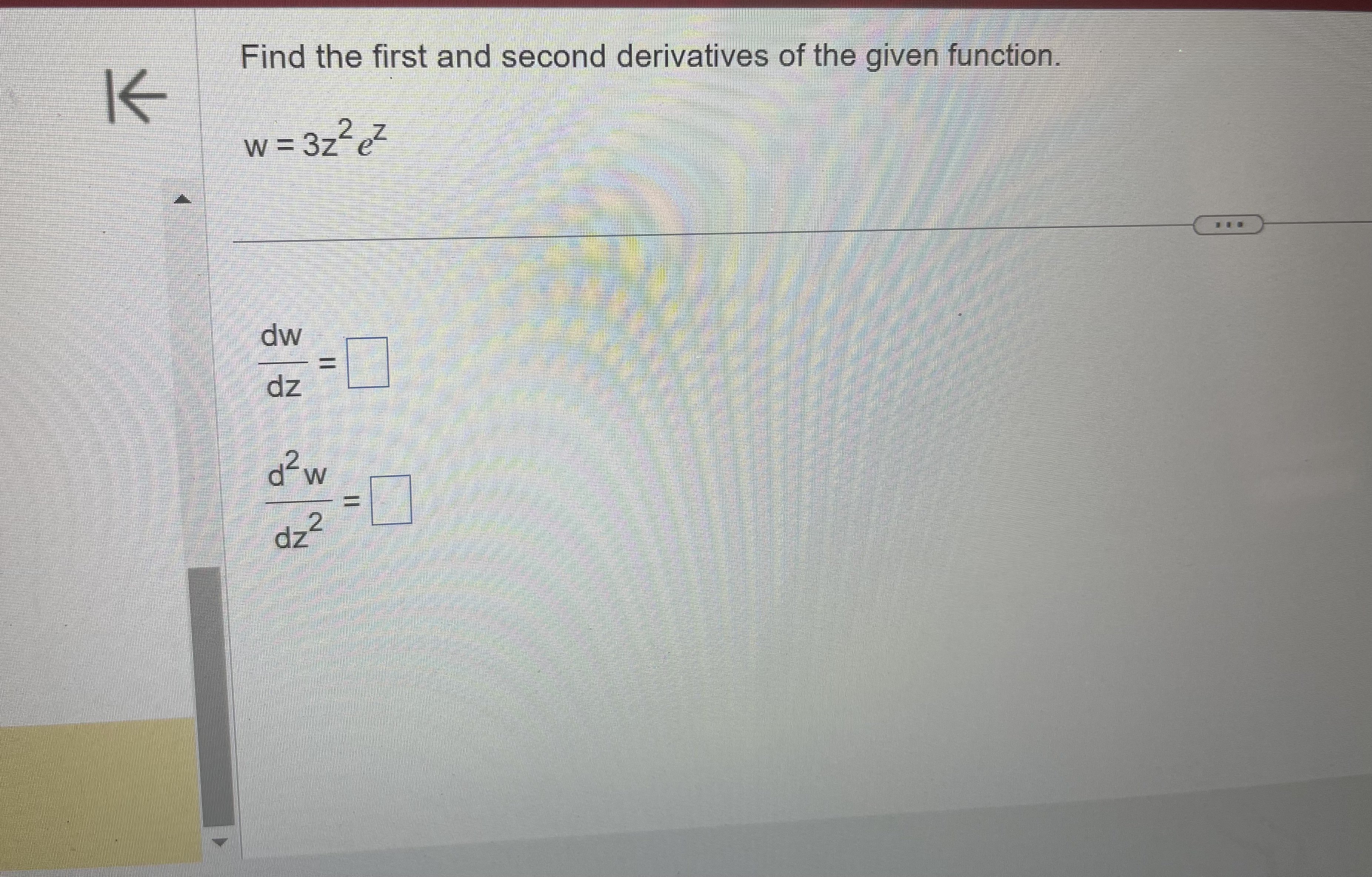
Does the parabola y = 3x- - 20x + 8 have a tangent whose slope is - 2? If so, find an equation for the line and the point of tangency. If not, why not? Select the correct choice below and, if necessary, fill in the answer boxes within your choice. O A. The parabola has a tangent whose slope is - 2. The equation of the tangent line is and the point of tangency is O B. The parabola does not have a tangent whose slope is - 2 because y does not have the value - 2 for any x-value in the domain of the curve. O C. The parabola does not have a tangent whose slope is - 2 because the equation of the tangent line does not have the value - 2 for any x-value in the domain of the curve. O D. The parabola does not have a tangent whose slope is - 2 because y' does not have the value - 2 for any x-value in the domain of the curve.K Find the first and second derivatives of the given function. W = 3zzez dw dz d2 w dzz -L