Question: Duration problems Problem 1 Consider a bond that has an annual coupon rate of 5% (semi-annually), five years to maturity, and is currently priced to

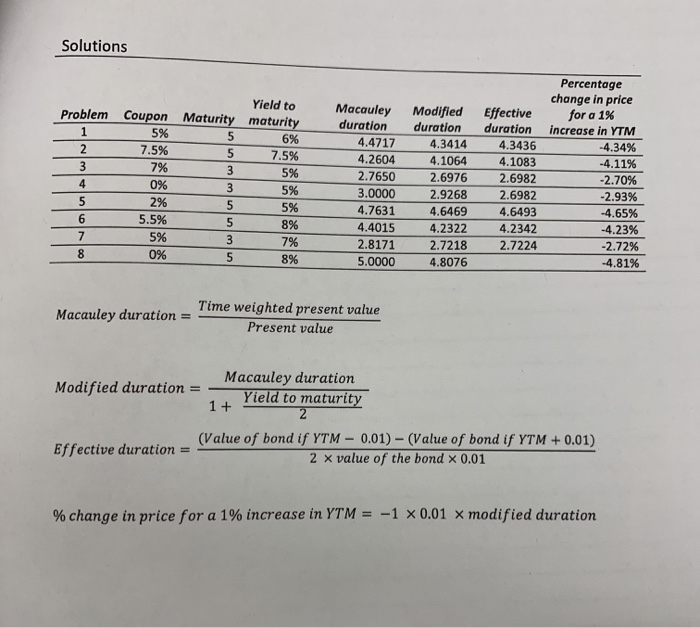
Duration problems Problem 1 Consider a bond that has an annual coupon rate of 5% (semi-annually), five years to maturity, and is currently priced to yield 6%. Calculate the following: CPNS Macauley duration Rv=100 Modified duration YL M = 6 Effective duration Stears Percentage change in price for a 1% increase in the yield to maturity Problem 2 Consider a bond that has an annual coupon rate of 7.5% (semi-annually), five years to maturity, and is currently priced to yield 7.5%. Calculate the following: CPN = 7.5 RV 1000 Macauley duration . Modified duration YLM = 7.5 Effective duration Stears Percentage change in price for a 1% increase in the yield to maturity Problem 3 Consider a bond that has an annual coupon rate of 7% (semi-annually), three years to maturity, and is currently priced to yield 5%. Calculate the following: Macauley duration Modified duration Effective duration Percentage change in price for a 1% increase in the yield to maturity Problem 4 Consider a zero coupon bond wth three years to maturity, and is currently priced to yield 5%. Calculate the following: Macauley duration Modified duration Effective duration Percentage change in price for a 1% increase in the yield to maturity Solutions Yield to Problem Coupon Maturity maturity 15% 56% 2 7 .5% 5 7.5% 37% 35% 0% 3 5% 2% 5 5 % 5.5% 5 8 % 5% 3 7 % 8 0% 5 8 % Macauley duration 4.4717 4.2604 2.7650 3.0000 4.7631 4.4015 2.8171 5.0000 Modified Effective duration duration 4.3414 4.3436 4.1064 4.1083 2.6976 2.6982 2.9268 2.6982 4.64694.6493 4.2322 4.2342 2.7218 2.7224 4.8076 Percentage change in price for a 1% increase in YTM -4.34% 4.11% -2.70% -2.93% -4.65% -4.23% -2.72% 4.81% Macauley duration = Time weighted present value Present value Macauley duration Modified duration = - 1+ Yield to maturity Effective duration = (Value of bond if YTM - 0.01) - (Value of bond if YTM + 0.01) 2 x value of the bond x 0.01 % change in price for a 1% increase in YTM = -1 x 0.01 x modified duration Duration problems Problem 1 Consider a bond that has an annual coupon rate of 5% (semi-annually), five years to maturity, and is currently priced to yield 6%. Calculate the following: CPNS Macauley duration Rv=100 Modified duration YL M = 6 Effective duration Stears Percentage change in price for a 1% increase in the yield to maturity Problem 2 Consider a bond that has an annual coupon rate of 7.5% (semi-annually), five years to maturity, and is currently priced to yield 7.5%. Calculate the following: CPN = 7.5 RV 1000 Macauley duration . Modified duration YLM = 7.5 Effective duration Stears Percentage change in price for a 1% increase in the yield to maturity Problem 3 Consider a bond that has an annual coupon rate of 7% (semi-annually), three years to maturity, and is currently priced to yield 5%. Calculate the following: Macauley duration Modified duration Effective duration Percentage change in price for a 1% increase in the yield to maturity Problem 4 Consider a zero coupon bond wth three years to maturity, and is currently priced to yield 5%. Calculate the following: Macauley duration Modified duration Effective duration Percentage change in price for a 1% increase in the yield to maturity Solutions Yield to Problem Coupon Maturity maturity 15% 56% 2 7 .5% 5 7.5% 37% 35% 0% 3 5% 2% 5 5 % 5.5% 5 8 % 5% 3 7 % 8 0% 5 8 % Macauley duration 4.4717 4.2604 2.7650 3.0000 4.7631 4.4015 2.8171 5.0000 Modified Effective duration duration 4.3414 4.3436 4.1064 4.1083 2.6976 2.6982 2.9268 2.6982 4.64694.6493 4.2322 4.2342 2.7218 2.7224 4.8076 Percentage change in price for a 1% increase in YTM -4.34% 4.11% -2.70% -2.93% -4.65% -4.23% -2.72% 4.81% Macauley duration = Time weighted present value Present value Macauley duration Modified duration = - 1+ Yield to maturity Effective duration = (Value of bond if YTM - 0.01) - (Value of bond if YTM + 0.01) 2 x value of the bond x 0.01 % change in price for a 1% increase in YTM = -1 x 0.01 x modified duration
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


