During our conversation about Stacks, Queues, and Deques, we talked about the circular array implementation of a queue. 1. Why didn't we need a circular array implementation of a stack? What quality, specifically, does a queue have that led to a need for the circular array implementation? (You need to be specific here, but it shouldn't require more than a sentence of two to answer this.) 2. You've seen that the dynamically-allocated array underlying a std::vector is resized periodically. Propose an algorithm for resizing the array used in the circular array implementation of a queue when it comes time to enqueue an element and the array is full. How much larger is your new array? How do the contents of your queue look different than before? 3. Assuming your algorithm was used to solve the problem of resizing the array when it's full, what is the amortized running time of the enqueue operation?

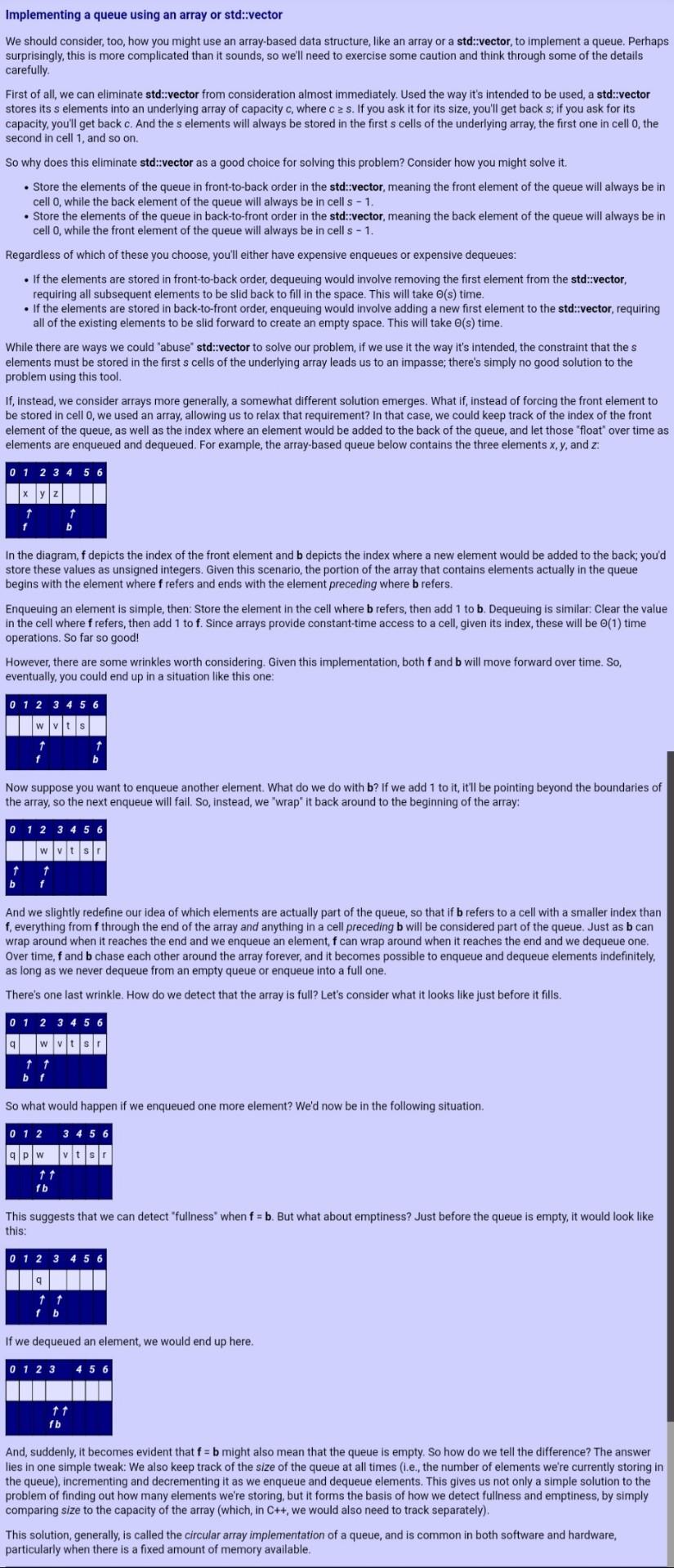
Implementing a queue using an array or std::vector We should consider, too, how you might use an array-based data structure, like an array or a std::vector, to implement a queue. Perhaps surprisingly, this is more complicated than it sounds, so we'll need to exercise some caution and think through some of the details carefully First of all, we can eliminate std::vector from consideration almost immediately. Used the way it's intended to be used, a std::vector stores its s elements into an underlying array of capacity c, where c 2 s. If you ask it for its size, you'll get back s, if you ask for its capacity, you'll get back c. And the s elements will always be stored in the first s cells of the underlying array, the first one in cell O, the second in cell 1, and so on. So why does this eliminate std::vector as a good choice for solving this problem? Consider how you might solve it. Store the elements of the queue in front-to-back order in the std::vector, meaning the front element of the queue will always be in cell O, while the back element of the queue will always be in cells - 1. Store the elements of the queue in back-to-front order in the std::vector, meaning the back element of the queue will always be in cell O, while the front element of the queue will always be in cells - 1. Regardless of which of these you choose, you'll either have expensive enqueues or expensive dequeues: If the elements are stored in front-to-back order, dequeuing would involve removing the first element from the std::vector, requiring all subsequent elements to be slid back to fill in the space. This will take o(s) time. If the elements are stored in back-to-front order, enqueuing would involve adding a new first element to the std::vector, requiring all of the existing elements to be slid forward to create an empty space. This will take o(s) time. While there are ways we could abuse' std::vector to solve our problem, if we use it the way it's intended, the constraint that the s elements must be stored in the first s cells of the underlying array leads us to an impasse; there's simply no good solution to the problem this tool. If, instead, we consider arrays more generally, a somewhat different solution emerges. What if, instead of forcing the front element to be stored in cello, we used an array, allowing us to relax that requirement? In that case, we could keep track of the index of the front element of the queue, as well as the index where an element would be added to the back of the queue, and let those "float' over time as elements are enqueued and dequeued. For example, the array-based queue below contains the three elements x,y, and z: 0 1 2 3 4 5 6 b In the diagram, f depicts the index of the front element and b depicts the index where a new element would be added to the back, you'd store these values as unsigned integers. Given this scenario, the portion of the array that contains elements actually in the queue begins with the element where f refers and ends with the element preceding where b refers. Enqueuing an element is simple, then: Store the element in the cell where b refers, then add 1 to b. Dequeuing is similar. Clear the value in the cell where f refers, then add 1 to f. Since arrays provide constant-time access to a cell, given its index, these will be o(1) time operations. So far so good! However, there are some wrinkles worth considering. Given this implementation, both f and b will move forward over time. So, eventually, you could end up in a situation like this one: 0 1 2 3 4 5 6 Now suppose you want to enqueue another element. What do we do with b? If we add 1 to it, it'll be pointing beyond the boundaries of the array, so the next enqueue will fail. So, instead, we 'wrap" it back around to the beginning of the array: 0 1 2 3 4 5 6 w vits b And we slightly redefine our idea of which elements are actually part of the queue, so that if b refers to a cell with a smaller index than f, everything from f through the end of the array and anything in a cell preceding b will be considered part of the queue. Just as b can wrap around when it reaches the end and we enqueue an element, f can wrap around when it reaches the end and we dequeue one. Over time, f and b chase each other around the array forever, and it becomes possible to enqueue and dequeue elements indefinitely, as long as we never dequeue from an empty queue or enqueue into a full one. There's one last wrinkle. How do we detect that the array is full? Let's consider what it looks like just before it fills. 0 1 2 3 4 5 6 9 wv b f So what would happen if we enqueued one more element? We'd now be in the following situation. 0 1 2 3 4 5 6 90 1 1 fb This suggests that we can detect "fullness when f = b. But what about emptiness? Just before the queue is empty, it would look like this: 0 1 2 3 4 5 6 fb If we dequeued an element, we would end up here. 0 1 2 3 4 5 6 11 fb And, suddenly, it becomes evident that f= b might also mean that the queue is empty. So how do we tell the difference? The answer lies in one simple tweak: We also keep track of the size of the queue at all times (1.e., the number of elements we're currently storing in the queue), incrementing and decrementing it as we enqueue and dequeue elements. This gives us not only a simple solution to the problem of finding out how many elements we're storing, but it forms the basis of how we detect fullness and emptiness, by simply comparing size to the capacity of the array (which, in C++, we would also need to track separately). This solution, generally, is called the circular array implementation of a queue, and is common in both software and hardware, particularly when there is a fixed amount of memory available