Dynamic Programing - City Planning. A city planner is asked to organize grocery shops in a new city. The city has a straight line main street that goes throughout the city. The city planner is asked to position where should the city provide permits to build new grocery shops so that people of the new city can have the shortest distance to their grocery markets. The population density is not constant along both sides of the main street. A higher density is around multiple city centers or crossroads along side the main street.

Your task is to develop an algorithm, given the positions of the city centers and the number of grocery shops, computes the least possible sum of all distances between each city centers and its nearest grocery shop.

Input to your Algorithm:

1. List of city centers coordinate positions along the main street (each an integer number
2. between 1 and 1000). This is a sequence of numbers.
3. Number of city centers is an integer between 2 and 100.
4. Number of grocery shops (an integer number between 2 and 30).
5. The number of shops is smaller than the number of city centers.

Output of your algorithm: A single integer, which is the sum of all distances between each city center and its nearest grocery market.

Sample Input:

5

[1 2 3 6 7 9 11 21 40 50]

Sample Output:

9

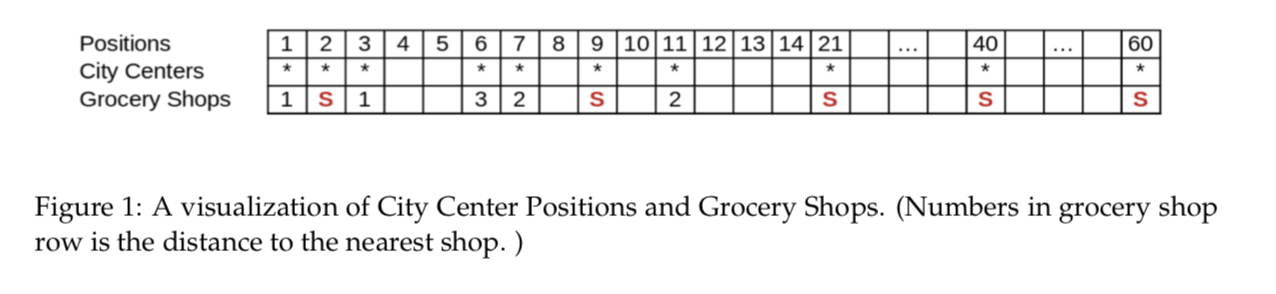
Tasks:

• Task 2.1. What are the sub-problems in this case? What is the counts of sub-problems? Provide a brief description of your solution.
• Task 2.2. Write up your algorithm in Pseudocode or python implementation.
• Task 2.3. What is the run time complexity of your algorithm?

Listing 1: This is a python program template to help you with your DP algorithm. Some parts are replaced with three question marks "???".

4 | 5 6 7 8 9 10 11 12 13 1421 40 60 1 2 3 * * * * * * * Positions City Centers Grocery Shops * 1s 1 3 2 s 2 S S S Figure 1: A visualization of City Center Positions and Grocery Shops. (Numbers in grocery shop row is the distance to the nearest shop. ) def grocery Shops (A, k): if not A: return 0 n = len (A) if k >= n : return 0 A. sort() # sort it if not sorted. dp[i][j] is the minimum cost for the first j city centers with i shops euclidean[i][j] is the euclidean distance between two city centers. euclidean[i][j] = euclidean[i][j - 1] + abs (A[ j - 1] - A[i - 1]) s[i][j] is the position of last shop we put to get dp[i][j]. dp = [[0 for - in range (n + 1)] for in range (k + 1)] euclidean = [[O for - in range(n + 1)] for in range(n + 1)] S = [[O for - in range(n + 1)] for - in range (n + 1)] for i in range(1, n + 1): for j in range(1, n + 1): euclidean[i][j] = euclidean[i][j - 1] + abs (A[ j - 1] - A[i - 1]) # Get the median a geometic median here. def get.median (i, j): k = int(i + (j - i) / 2) return euclidean[k][j] - euclidean[k][i - 1] for i in range(1, n + 1): dp [1][i] = get-median (1, i) for i in range (1, n + 1) : build a shop at each city center. s[i][i] = i # Generate the DP table. for i in range (2, k + 1): j = n dp[i][j] = float('inf') enumerate k from s[i - 1][j] to j - 1. As the following loops don't calculate the situation when j = n. for k in range (s[i 1][j], j): temp = dp[i - 1][k] + ??? if temp > 9 4 | 5 6 7 8 9 10 11 12 13 1421 40 60 1 2 3 * * * * * * * Positions City Centers Grocery Shops * 1s 1 3 2 s 2 S S S Figure 1: A visualization of City Center Positions and Grocery Shops. (Numbers in grocery shop row is the distance to the nearest shop. ) def grocery Shops (A, k): if not A: return 0 n = len (A) if k >= n : return 0 A. sort() # sort it if not sorted. dp[i][j] is the minimum cost for the first j city centers with i shops euclidean[i][j] is the euclidean distance between two city centers. euclidean[i][j] = euclidean[i][j - 1] + abs (A[ j - 1] - A[i - 1]) s[i][j] is the position of last shop we put to get dp[i][j]. dp = [[0 for - in range (n + 1)] for in range (k + 1)] euclidean = [[O for - in range(n + 1)] for in range(n + 1)] S = [[O for - in range(n + 1)] for - in range (n + 1)] for i in range(1, n + 1): for j in range(1, n + 1): euclidean[i][j] = euclidean[i][j - 1] + abs (A[ j - 1] - A[i - 1]) # Get the median a geometic median here. def get.median (i, j): k = int(i + (j - i) / 2) return euclidean[k][j] - euclidean[k][i - 1] for i in range(1, n + 1): dp [1][i] = get-median (1, i) for i in range (1, n + 1) : build a shop at each city center. s[i][i] = i # Generate the DP table. for i in range (2, k + 1): j = n dp[i][j] = float('inf') enumerate k from s[i - 1][j] to j - 1. As the following loops don't calculate the situation when j = n. for k in range (s[i 1][j], j): temp = dp[i - 1][k] + ??? if temp > 9