Dynamical systems.

using that to solve them ,please both parts

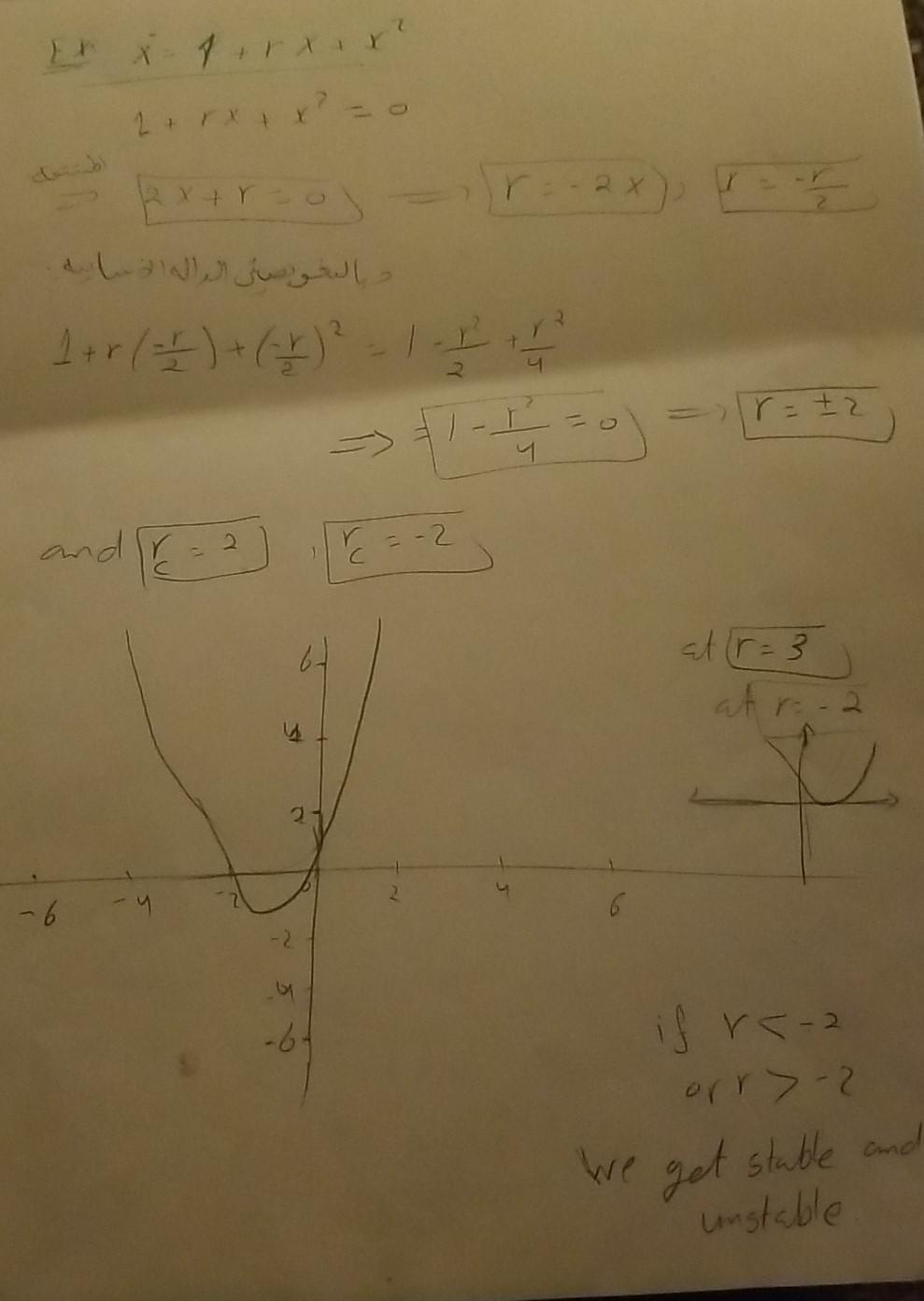
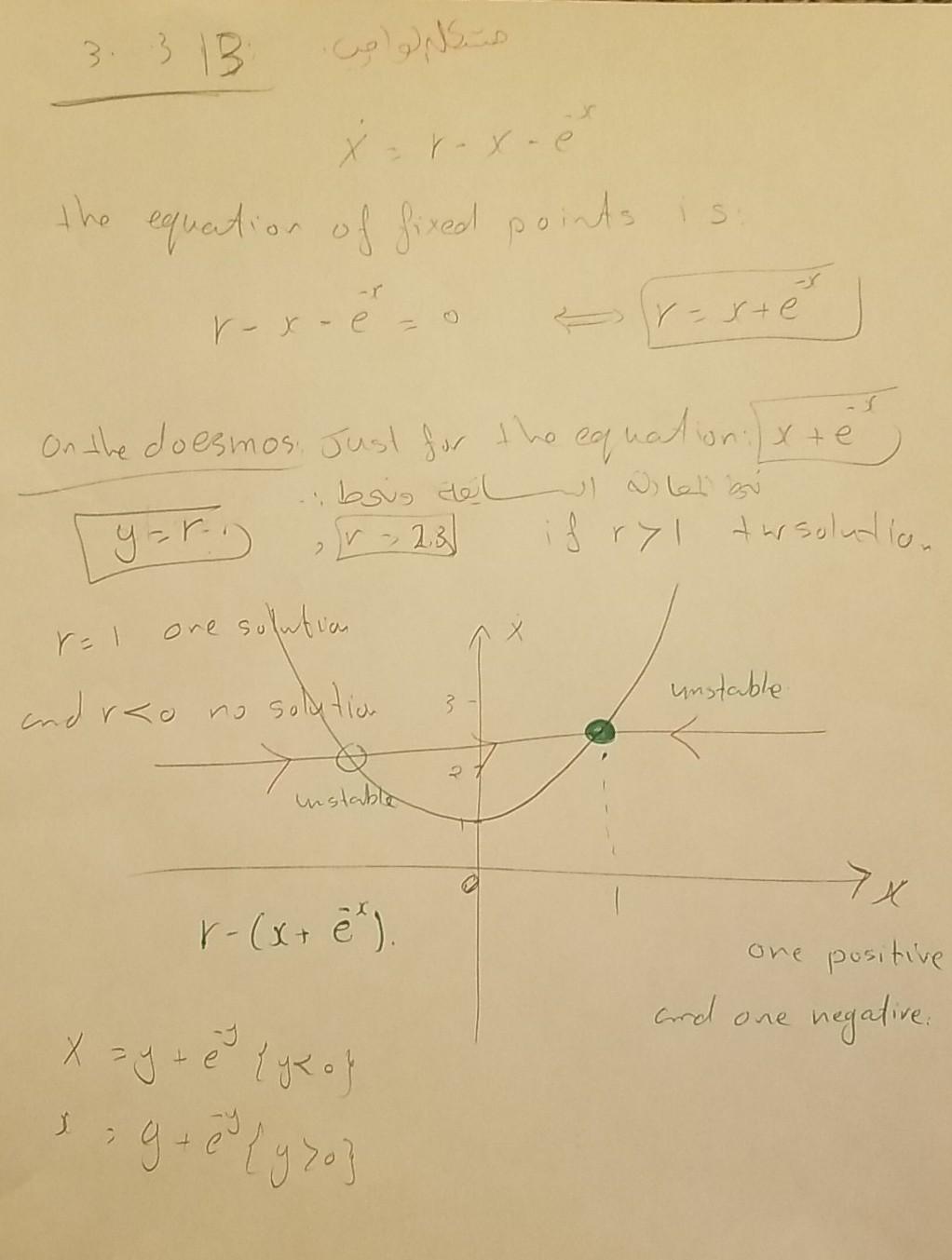
3.4.13 (Computer work on bifurcation diagrams) For the vector fields below, use a computer to obtain a quantitatively accurate plot of the values of x* vs. r, where 0 Sr 53. In each case, there's an easy way to do this, and a harder way us- ing the Newton-Raphson method. a) i=r-x-es b) i=1-x-e 3.3 13 X-r-x- the equation of fixed points is r-x-e-o r - ste On the doesmos. Just for the equation:) x + e oo r 22.30 if ryl tur solution one solution yar. 2 unstable andrco no solution unstable 7x r-(x + et one positive and one negative . x = y + { K of g+ es {y zo} S 2 Xrx? 2 + rx x Rxtro ) 3 1 ++ ( =/ ) + (+) = r=+2 => -1 and r = 2 r = -2 at (r=3 atra P 2 -6 - 2 if re- orr-2 We get stable and unstable 5. Problem 3.4.13 (UG) You can use either Jupyter or Desmos for this. Ignore the comment about the Newton-Raphson method