e $=(\text{'}*\text{'},2,(\text{'}+\text{'},\text{'}$x$\text{'},1))$

import math

import random

class IllegalOperator$($Exception$)$:

pass

def calc$($op$,$ left, right$)$:

if op $=="+"$:

return left $+$ right

elif op $=="-"$:

return left $-$ right

elif op $=="*"$:

return left $*$ right

elif op $=="/"$:

return left $/$ right

else:

raise IllegalOperator$($op$)$

def compute$($e$)$:

if isinstance$($e$,$ tuple$)$:

# We have an expression.

op$,$ l$,$ r $=$ e

# We compute the subexpressions.

ll $=$ compute$($l$)$

rr $=$ compute$($r$)$

# And on the basis of those, the whole expression.

return calc$($op$,$ ll$,$ rr$)$

else:

# base expression; just return the number.

return e

from numbers import Number # The mother class of all numbers.

def isnumber$($e$)$:

return isinstance$($e$,$ Number$)$

def isvariable$($e$)$:

return isinstance$($e$,$ str$)$

def iscomposite$($e$)$:

return isinstance$($e$,$ tuple$)$

def simplify$($e$)$:

if isinstance$($e$,$ tuple$)$:

op$,$ l$,$ r $=$ e

# We simplify the children expressions.

ll $=$ simplify$($l$)$

rr $=$ simplify$($r$)$

# We compute the expression if we can.

if isnumber$($ll$)$ and isnumber$($rr$)$:

return calc$($op$,$ ll$,$ rr$)$

else:

return $($op$,$ ll$,$ rr$)$

else:

# Leaf. No simplification is possible.

return e

varval $=\{\text{'}$x$\text{'}$: $3,\text{'}$y$\text{'}$: $8\}$

#@title Evaluating an expression with respect to a variable evaluation

def compute$($e$,$ varval$=\{\})$:

varval $=$ varval

if isnumber$($e$)$:

return e

elif isvariable$($e$)$:

if varval.get$($e$)!=$ None:

return varval.get$($e$)$

else:

return e

else:

op$,$ l$,$ r $=$ e

ll $=$ compute$($l$,$ varval$)$

rr $=$ compute$($r$,$ varval$)$

if isnumber$($ll$)$ and isnumber$($rr$)$:

return calc$($op$,$ ll$,$ rr$)$

else:

return $($op$,$ ll$,$ rr$)$

#@title Exercise: define $`$variables$`$

def variables$($e$,$ l$1=$ None$)$:

if l$1$ is None:

l$1=$ set$()$

if isvariable$($e$)$:

l$1.$add$($e$)$

elif iscomposite$($e$)$:

op$,$ l$,$ r $=$ e

variables$($l$,$ l$1)$

variables$($r$,$ l$1)$

return set$($l$1)$

#@title Exercise: implementation of value equality

def value$\_$equality$($e$,$ f$,$ num$\_$samples$=1000,$ tolerance$=1$e$-6)$:

$"""$Return True if the two expressions self and other are numerically

equivalent. Equivalence is tested by generating

num$\_$samples assignments, and checking that equality holds

for all of them. Equality is checked up to tolerance, that is$,$

the values of the two expressions have to be closer than tolerance.

It can be done in less than $10$ lines of code."""

vars $=$ variables$($e$)|$ variables$($f$)$

for i in range$($num$\_$samples$)$:

map $=\{\}$

for a in vars:

map$[$a$]=$ random.gauss$(0,10)$

if abs$($compute$($e$,$ map$)-$ compute$($f$,$ map$))$ tolerance:

return True

return False

#@title Derivation of a leaf expression

def derivate$\_$leaf$($e$,$ x$)$:

$"""$This function takes as input an expression e and a variable x$,$

and returns the symbolic derivative of e wrt$.$ x$,$ as an expression."""

return $1$ if e $==$ x else $0$

#@title Implement $`$derivate$`$

def derivate$($e$,$ x$)$:

$"""$Returns the derivative of e wrt x$.$

It can be done in less than $15$ lines of code."""

if iscomposite$($e$)$:

op$,$ l$,$ r $=$ e

if op $==\text{'}+\text{'}$ or op $==\text{'}-\text{'}$:

return $($op$,$ derivate$($l$,$ x$),$ derivate$($r$,$ x$))$

elif op $==\text{'}*\text{'}$:

return $(\text{'}+\text{'},($op$,$ derivate$($l$,$ x$),$ r$),($op$,$ l$,$ derivate$($r$,$ x$)))$

elif op $==\text{'}/\text{'}$:

return $($op$,(\text{'}-\text{'},(\text{'}*\text{'},$ derivate$($l$,$ x$),$ r$),(\text{'}*\text{'},$ l$,$ derivate$($r$,$ x$))),(\text{'}*\text{'},$ r$,$ r$))$

else:

return derivate$\_$leaf$($e$,$ x$)$

def derivate$\_$approx$($f$,$ x$,$ varval, delta$=0\mathrm{.}0001)$:

$"""$Computes the derivative of f with respect to x$,$ for a given delta,

using the $($f$($x $+$ delta$)-$ f$($x$))/$ delta method. $"""$

# This is f$($x$)$

f$\_$x $=$ compute$($f$,$ varval$=$varval$)$

varval$\_$delta $=$ dict$($varval$)$

varval$\_$delta$[$x$]+=$ delta

# This is f$($x $+$ delta$)$

f$\_$x$\_$plus$\_$delta $=$ compute$($f$,$ varval$=$varval$\_$delta$)$

return $($f$\_$x$\_$plus$\_$delta $-$ f$\_$x$)/$ delta

def similar$($x$,$ y$,$ epsilon$)$:

if x $<mtext\; id="EditorElement\_1210972"></mtext><mn\; id="EditorElement\_1210973">0</mn>$ and y $<mtext\; id="EditorElement\_1210982"></mtext><mn\; id="EditorElement\_1210983">0</mn>$:

# If they are negative, max and min play opposite roles.

return similar$(-$x$,-$y$,$ epsilon$)$

if abs$($x $-$ y$)$ epsilon:

return True

else:

return max$($x$,$ y$)/($min$($x$,$ y$)+$ epsilon epsilon

#@title Implementation of $`$test$\_$derivative$`$

def test$\_$derivative$($f$,$ df$,$ x$,$ delta$=0\mathrm{.}0001,$ tolerance$=0\mathrm{.}01,$ num$\_$tests$=1000)$:

$"""$Tests if the derivative of f with respect to x is approximately equal to df$.$

Returns True if the test passes for all randomly generated inputs, False otherwise."""

## YOUR SOLUTION HERE

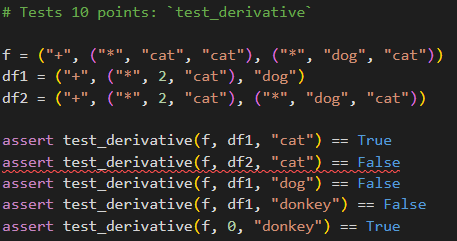
Please implement def test$\_$derivative$($f$,$ df$,$ x$,$ delta$=0\mathrm{.}0001,$ tolerance$=0\mathrm{.}01,$ num$\_$tests$=1000).$ You cannot import anything new or create$/$delete any existing methods. This method must pass the following test $($in picture$)$:

# Tests $10$ points: 'test$\_$derivative'

$f=(+,(,$ cat, cat$),(*,$ dog, cat$))$

$df1=(+,(*,2,$ cat$),$ dog$)$

$df2=(+,(*,2,$ cat$),(*,$ dog, cat$))$

assert test$\_$st: