E$4.$ Suppose an encoder RS $(7,3)$ transmitting the output codeword U$($X$)=(110001$

$010010110101001).$ However, the codeword received is r$($X$)=(110001010010110$

$010110).$

a$)$ Determine the value of the syndrome for each roots of the generator

polynomial g$($X$)$

b$)$ Determine the error localization

$2$

c$)$ Determine the value of the error symbol

d$)$ Determine the correct codeword

Sol: a$)$ S$1=\backslash$alpha $6$

$,$ S$2=\backslash$alpha $0$

$,$ S$3=\backslash$alpha $0$

$,$ S$4=\backslash$alpha $2$

; b$)()=\backslash$alpha $0$

$+\backslash$alpha $1$

X $+\backslash$alpha $4$

X$2$

; c$)$ e$($X$)=\backslash$alpha $5$

X$5$

$+\backslash$alpha $5$

X$6$

;

d$)*($X$)=(\backslash$alpha $3$

$,\backslash$alpha $2$

$,\backslash$alpha $1$

$,\backslash$alpha $1$

$,\backslash$alpha $3$

$,\backslash$alpha $6$

$,\backslash$alpha $2$

$)$

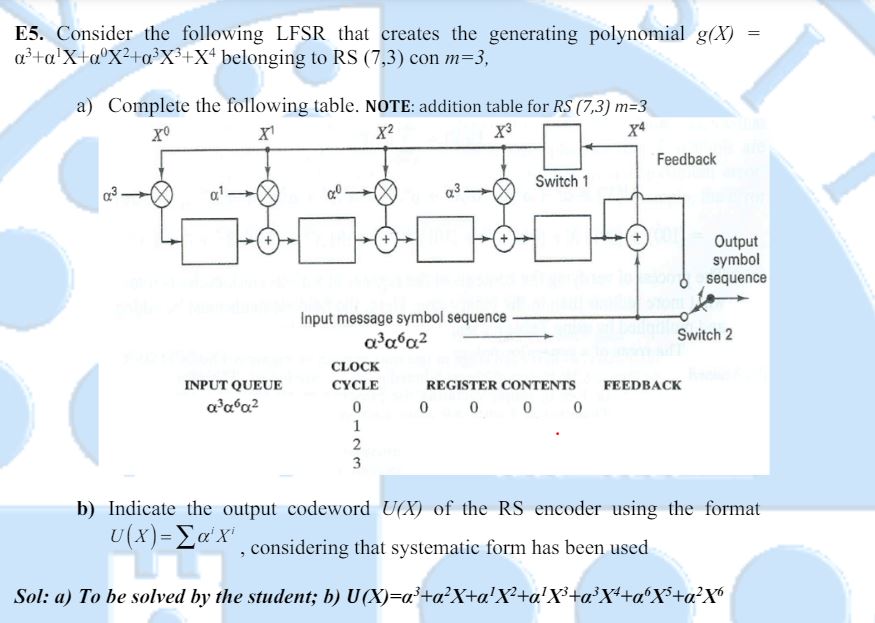
E$5.$ Consider the following LFSR that creates the generating polynomial g$($X$)=$

$\backslash$alpha $3$

$+\backslash$alpha $1$

X$+\backslash$alpha $0$

X$2$

$+\backslash$alpha $3$

X$3$

$+$X$4$ belonging to RS $(7,3)$ con m$=3,$

a$)$ Complete the following table. NOTE: addition table for RS $(7,3)$ m$=3$

b$)$ Indicate the output codeword U$($X$)$ of the RS encoder using the format

$,$ considering that systematic form has been used

Sol: a$)$ To be solved by the student; b$)($X$)=\backslash$alpha $3$

$+\backslash$alpha $2$

X$+\backslash$alpha $1$

X$2$

$+\backslash$alpha $1$

X$3$

$+\backslash$alpha $3$

X$4$

$+\backslash$alpha $6$

X$5$

$+\backslash$alpha $2$

X$6$

E$6.$ Suppose an entertainment company that designs a new coding protocol based on

Reed Solomon, specifically $($n$,$k$)=(15,9)$ in which each data symbol is composed of

m$=4$ bits. If the primitive polynomial f$($X$)=1+$X$+$X$4$

$,$

a$)$ Represent graphically the primitive polynomial f$($X$)$ using registers LFSR$.$

Detail within each register E$0,$ E$1,...$ assuming that E$0$ represents the

leftmost register

b$)$ Compute the values ai needed of the addition table GF$(2$m$)$

c$)$ Compute all the values ai of the multiplication table GF$(2$m$)$ for the variables

a$13$ y a$14$

d$)$ Compute the polynomial generator g$($X$)$ providing the solution in the most

simplified expression

Sol: a$)$ To be solved by the student; b$)$ To be solved by the student; c$)$ To be solved by

the student; d$)$ g$($X$)=\backslash$alpha $6$

$+\backslash$alpha $9$

X$+\backslash$alpha $6$

X$2$

$+\backslash$alpha $4$

X$3$

$+\backslash$alpha $14$X$4$

$+\backslash$alpha $10$X$5$

$+$X$6$E$5.$ Consider the following LFSR that creates the generating polynomial $g(x)=$

${}^3+{}^{1}x+{}^0{x}^2+{}^3{x}^3+x^4$ belonging to $RS(7,3)$ con $m=3,$

a$)$ Complete the following table. NOTE: addition table for $RS(7,3)m=3$

b$)$ Indicate the output codeword $U(x)$ of the RS encoder using the format

$U(x)={\displaystyle \underset{?}{\overset{?}{}}}{}^i{x}^i,$ considering that systematic form has been used

Sol: a$)$ To be solved by the student; b$)U(x)={}^3+{}^{2}x+{}^1{x}^2+{}^1{x}^3+{}^3{x}^4+{}^6{x}^5+{}^2{x}^6$

Please I need someone to explain to me in details in finding solution