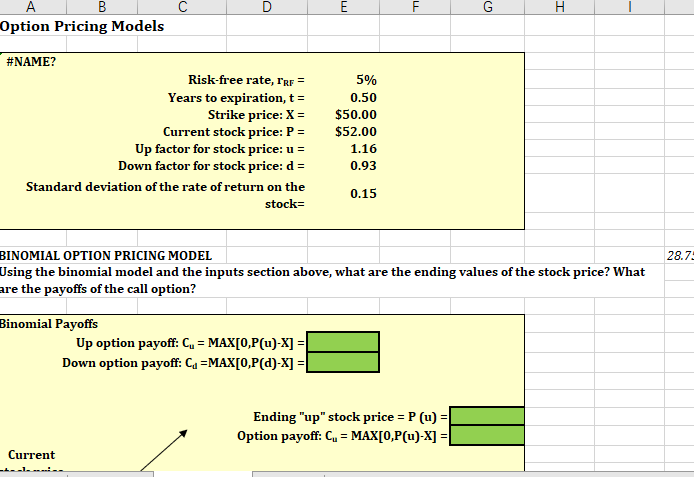
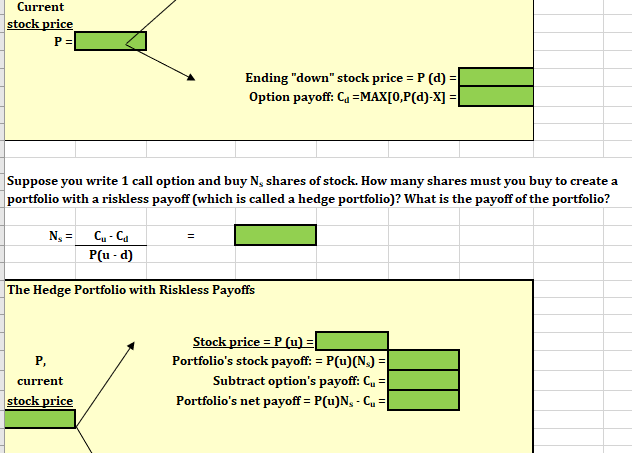
E F G H A B Option Pricing Models #NAME? Risk-free rate, l'rr = Years to expiration, t = Strike price: X = Current stock price: P = Up factor for stock price: u = Down factor for stock price: d = Standard deviation of the rate of return on the stock- 5% 0.50 $50.00 $52.00 1.16 0.93 0.15 28.7: BINOMIAL OPTION PRICING MODEL Using the binomial model and the inputs section above, what are the ending values of the stock price? What are the payoffs of the call option? Binomial Payoffs Up option payoff: C. = MAX[0,P(u)-X] = Down option payoff: Cu =MAX[0,P(a)-X] = Ending "up" stock price = P (u) = Option payoff: C. = MAX[0,P(u)-X] = Current Current stock price P= Ending "down" stock price = P(a) Option payoff: Cu =MAX[0,P(d)-X] = Suppose you write 1 call option and buy N, shares of stock. How many shares must you buy to create a portfolio with a riskless payoff (which is called a hedge portfolio)? What is the payoff of the portfolio? N = Cu-Cd P(u-d) The Hedge Portfolio with Riskless Payoffs P, current stock price Stock price = P (u) = Portfolio's stock payoff: = P(u)(N.) = Subtract option's payoff: Cu = Portfolio's net payoff = P(u)N-C= Stock price = P(a) = Portoflio's stock payoff: = P(d)(N.) = Subtract option's payoff: Cu = Portoflio's net payoff = P(d)N, - Cu = What is the present value of the riskless payoff disounted at the risk-free rate (we assume daily compounding) is: N= I/YR = PMT = FV = PV = The call value (Ve) is: Vc = N. (P) - Present value of riskless payoff VCI BLACK-SCHOLES OPTION PRICING MODEL What is the value of the following call option according to the Black-Scholes OPM? Use the inputs section above to solve for d. What is the value of the following call option according to the Black-Scholes OPM? Use the inputs section above to solve for d. (d) Having solved for di, now use this value to find dz. (dz) Using the NORMSDIST function, find N(01) and N(42) N(21) = N(D2) = Using Black-Scholes the call value (VC) is: Vc = E F G H A B Option Pricing Models #NAME? Risk-free rate, l'rr = Years to expiration, t = Strike price: X = Current stock price: P = Up factor for stock price: u = Down factor for stock price: d = Standard deviation of the rate of return on the stock- 5% 0.50 $50.00 $52.00 1.16 0.93 0.15 28.7: BINOMIAL OPTION PRICING MODEL Using the binomial model and the inputs section above, what are the ending values of the stock price? What are the payoffs of the call option? Binomial Payoffs Up option payoff: C. = MAX[0,P(u)-X] = Down option payoff: Cu =MAX[0,P(a)-X] = Ending "up" stock price = P (u) = Option payoff: C. = MAX[0,P(u)-X] = Current Current stock price P= Ending "down" stock price = P(a) Option payoff: Cu =MAX[0,P(d)-X] = Suppose you write 1 call option and buy N, shares of stock. How many shares must you buy to create a portfolio with a riskless payoff (which is called a hedge portfolio)? What is the payoff of the portfolio? N = Cu-Cd P(u-d) The Hedge Portfolio with Riskless Payoffs P, current stock price Stock price = P (u) = Portfolio's stock payoff: = P(u)(N.) = Subtract option's payoff: Cu = Portfolio's net payoff = P(u)N-C= Stock price = P(a) = Portoflio's stock payoff: = P(d)(N.) = Subtract option's payoff: Cu = Portoflio's net payoff = P(d)N, - Cu = What is the present value of the riskless payoff disounted at the risk-free rate (we assume daily compounding) is: N= I/YR = PMT = FV = PV = The call value (Ve) is: Vc = N. (P) - Present value of riskless payoff VCI BLACK-SCHOLES OPTION PRICING MODEL What is the value of the following call option according to the Black-Scholes OPM? Use the inputs section above to solve for d. What is the value of the following call option according to the Black-Scholes OPM? Use the inputs section above to solve for d. (d) Having solved for di, now use this value to find dz. (dz) Using the NORMSDIST function, find N(01) and N(42) N(21) = N(D2) = Using Black-Scholes the call value (VC) is: Vc =
